Can someone show me how to plot a rhumb line (loxodrome) in Mathematica via the ParametricPlot3D function?
Here is what I got so far:
ParametricPlot3D[{Cos[λ]/Cosh[Cot[π/4] λ], Sin[λ]/Cosh[Cot[π/4] λ], Tanh[Cot[π/4] λ]},
{λ, 0, π}]
I am trying to get this one:
Here's a version where you can manipulate the angle under which the meridians of longitude are crossed, using the k slider. To get the full loxodrome from pole to pole, you have to plot from $-2\pi/k$ to $2\pi/k$, which is done automatically here when a = 1.
Furthermore, you can influence which meridian is crossed by changing $\lambda_0$. This is the same as rotating the loxodrome.
Manipulate[Show[
Graphics3D[{Opacity[.4], Specularity[White, 30], Orange,
Sphere[{0, 0, 0}, .95]}],
ParametricPlot3D[{Cos[λ]/Cosh[k (λ - λ0)], Sin[λ]/Cosh[k (λ - λ0)], Tanh[k (λ - λ0)]},
{λ, -2 a π/k, 2 a π/k},
MaxRecursion -> ControlActive[3, 7], PlotPoints -> ControlActive[20, 50]
] /. l : Line[pts_] :> ControlActive[l, Tube[pts]],
SphericalRegion -> True
],
{k, -1, 1, .09},
{{a, 1}, .01, 1},
{λ0, 0, 2 π}
]
k needs to be in range from -0,5 to -0,005 and what does it stand for?
– Ivana
Jun 03 '13 at 00:34
k is defined as k=Cot[beta] where beta is the crossing angle. k's meaningful interval is maybe [-1,1] although it cannot be 0 (which is 90 degree) and close to 0 there are too many lines and the graphic gets slow. But you could of course use something like {k, -1, 1, .09} (cleverly overjumping the 0).
– halirutan
Jun 03 '13 at 00:44
Line with Tube. Tube was new in 7 and may not work as expected. You could remove the /.l:Line... part to test this. Then you could decrease the MaxRecursion and PlotPoints settings and if nothing helps even remove Opacity and Specularity.
– halirutan
Jun 03 '13 at 07:20
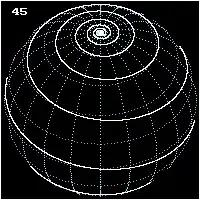
For a better presentation of the curve we would like to see also the background - in this case a sphere.
Let's use your definition of the curve with appropriate options, e.g. MeshFunctions -> {#3&} to visualize parallels.
Show[
ParametricPlot3D[ {Sin[u] Sin[v], Cos[u] Sin[v], Cos[v]},
{u, -Pi, Pi}, {v, -Pi, Pi}, MaxRecursion -> 4, PlotPoints -> 80,
PlotStyle -> { Lighter @ Blue, Specularity[Green, 10]}, Axes -> None,
Boxed -> False, Mesh -> 25, MeshFunctions -> {#3 &}],
ParametricPlot3D[{ Cos[ω]/Cosh[Cot[Pi/4]*ω], Sin[ω]/Cosh[Cot[Pi/4]*ω],
Tanh[Cot[Pi/4]*ω]}, {ω, 0, Pi},
PlotStyle -> {White, Thick}]]
Now it should be much easier to get any desired specific effects.
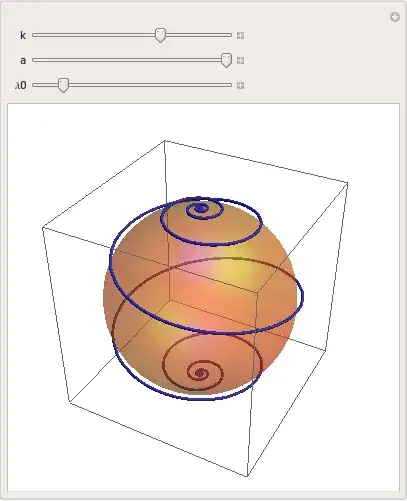
For more customized presentation we define a function drawing the loxodrome:
loxodrome[a_, b_, ω0_] /; 0.1 < a < Pi/2 && -1 < b < -0.01 && 0 < ω0 < 2 Pi :=
Show[
ParametricPlot3D[
{Sin[u] Sin[v], Cos[u] Sin[v], Cos[v]}, {u, -Pi, Pi}, {v, -Pi, Pi},
MaxRecursion -> 4, PlotPoints -> 80,
PlotStyle -> {Lighter@Blue, Specularity[Green, 10], Opacity[3/5]},
Axes -> None, Boxed -> False, Mesh -> {12, 12}, MeshFunctions -> {#3 &, #4 &},
MeshStyle -> {Dashed, Dashed}],
ParametricPlot3D[
{ Cos[ω]/Cosh[Cot[a](ω - ω0)], Sin[ω]/Cosh[Cot[a](ω - ω0)], Tanh[Cot[a](ω- ω0)]},
{ω, -2 Pi/b, 2 Pi/b}, PlotStyle -> {White, Thick} ]
]
Now we can manipulate the parameters, a, b and ω0, e.g. a determines inclination of the curve to parallels:
Manipulate[ loxodrome[a, b, ω0],
{{a, 3Pi/8}, 0.1, Pi/2}, {{ω0, Pi}, 0, 2 Pi}, {{b, -1/2}, -1, -0.01}]
or simply specify the arguments:
loxodrome[15 Pi/32, -1/8, 19 Pi/10]
Using the formulae from here, here is a way to plot the loxodrome of a general surface of revolution, specialized to the spherical case:
With[{α = π/4}, (* angle from the latitude *)
f[u_] := Cos[u]; g[u_] := Sin[u];
lox = DSolveValue[{l'[u] == Cot[α] (Sqrt[#.#] &[{f'[u], g'[u]}])/f[u], l[0] == -π/2},
l, u];
Show[RevolutionPlot3D[{f[u], g[u]}, {u, -π, π},
MeshStyle -> Directive[Thin, GrayLevel[1/4], Opacity[1/2]]],
ParametricPlot3D[{f[u] Cos[lox[u]], f[u] Sin[lox[u]], g[u]}, {u, -π, π}] /.
Line -> Tube]]
One can do something similar for the pseudosphere:
With[{α = π/12},
f[u_] := Sech[u]; g[u_] := u - Tanh[u];
lox = DSolveValue[{l'[u] == Cot[α] (Sqrt[#.#] &[{f'[u], g'[u]}])/f[u], l[0] == -π/2},
l, u];
Show[RevolutionPlot3D[{f[u], g[u]}, {u, -3, 3},
MeshStyle -> Directive[Thin, GrayLevel[1/4], Opacity[1/2]]],
ParametricPlot3D[{f[u] Cos[lox[u]], f[u] Sin[lox[u]], g[u]}, {u, -3, 3}] /.
Line -> Tube]]
(Of course, one can use NDSolveValue[] instead if the DE for the loxodrome does not have a closed form solution.)
AFAIK, loxodrome is the image under the stereographic projection transformation of a logarithmic spiral. So I use the following approach.
Suppose the sphere is Sphere[{0,0,1},1], and the stereographic projection is
stereoMap[{x_, y_}] =
Block[{t},
t {0, 0, 2} + (1 - t) {x, y, 0} /.
Solve[EuclideanDistance[
t {0, 0, 2} + (1 - t) {x, y, 0}, {0, 0, 1}] == 1 && t != 1,
t,Reals] // Simplify][[1]];
That is
$$\{x,y\}\mapsto \left\{\frac{4 x}{x^2+y^2+4},\frac{4 y}{x^2+y^2+4},\frac{2 \left(x^2+y^2\right)}{x^2+y^2+4}\right\}$$
angle0 = 50;
angle = 30;
logspiralMap[θ_] :=
With[{a = .05, b = .15},
a*E^(b*θ) {Cos[θ], Sin[θ]}];
logspiral2d =
ParametricPlot[logspiralMap[θ], {θ, 0, angle0},
PlotStyle -> Green, PlotRange -> All]
logspiral3d to the unit sphere by stereoMap.loxodromeMap = stereoMap@*logspiralMap;
pt = logspiralMap[angle];
qt = loxodromeMap[angle];
line = Graphics3D[{Red, Line[{{0, 0, 2}, PadRight[pt, 3]}],
PointSize[Large], Point[qt], Point[PadRight[pt, 3]]}];
logspiral3d =
ParametricPlot3D[
PadRight[logspiralMap[θ], 3], {θ, 0, angle},
PlotStyle -> Green];
loxodrom =
ParametricPlot3D[loxodromeMap[θ], {θ, 0, angle0},
PlotStyle -> Blue];
Show[logspiral3d, loxodrom, line,
Graphics3D[{Opacity[0.1], Sphere[{0, 0, 1}, 1]}],
ViewPoint -> {2.88, 0.33, 1.73}, ImageSize -> Large,
PlotRange -> All, Boxed -> False, Axes -> False]
loxodromes[a_, b_] :=
{2 a E^(b u) Cos[u],
2 a E^(b u) Sin[u],
a^2 E^(2 b u) - 1} / (1 + a^2 E^(2 b u))
Show[
ParametricPlot3D[
loxodromes[1, 0.1],
{u, -16 Pi, 16 Pi},
ColorFunction -> "Rainbow",
PlotStyle -> Thickness[0.01]],
Graphics3D[{Opacity[0.2], Sphere[]}]]
