Solution of differential equation by by an iterative method

Question

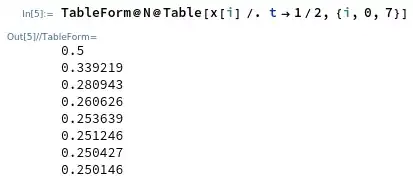
Let $y^{\prime\prime}(t)+y^{2}(t)-t^{4}-2=0$, where $0\leq t\leq 1$. The boundary conditions are $y(0)=0$ and $y(1)=1$ and so its exact solution is $y(t)=t^{2}$. Now I want to compute the solution by the following method; $x_{n}=x_{n-1}+\alpha_{n-1}\int_{0}^{t}s(1-t)[x^{\prime\prime}_{n-1}(s)+x^{2}_{n-1}(s)-s^{4}-2]ds+\alpha_{n-1}\int_{t}^{1}t(1-s)[x^{\prime\prime}_{n-1}(s)+x^{2}_{n-1}(s)-s^{4}-2]ds$ $n=0,1,2,..$ where the initial guess is $x_{0}(t)=t$. I have set the following code for $t=0.5$ so the exact solution in this case is $y(t)=0.5^{2}=0.25$ and $x_{0}(t)=t=0.5$. Now I set the following code:

Clear[x,s, T, a]
a[n_] := a[n] = 0.70
t=0.5
x[0] = 0.5;
x[n_] := x[n] = x[n-1]+a[n-1]Integrate[s(1-t)(x''[n-1]+(x[n-1])^2-s^4-2),{s,0,t}]
+a[n-1]Integrate[t(1-s)(x''[n-1]+(x[n-1])^2-s^4-2),{s,t,1}]
NumberForm[a1 = {Table[x[i], {i, 0, 7}]}, 5]

and when I run the mathemtica I found some error. Please help me.

Answer 1

Below the trick is to use Interpolation, which can transform discrete values into a continuous function, so that the latter can be Derivatived directly and the difficulty mentioned by @DaneilHuber in the comment is overcome.

Clear[ndSolveByIterate]
ndSolveByIterate[tsamplings_, xinitfunc_] := 
Module[{xinit = xinitfunc /@ tsamplings, α = .7, Δx, iterate, zero = 1.*^-4},
  Δx[t_, xlast_] := 
  Module[{xfunc = Interpolation[{tsamplings, xlast}\[Transpose]], integrand},
    integrand[s_] := xfunc''[s] + xfunc[s]^2 - s^4 - 2;
    α (NIntegrate[s (1 - t) integrand[s], {s, 0, t}] + 
       NIntegrate[t (1 - s) integrand[s], {s, t, 1}])
  ];
  iterate = # + ParallelTable[Δx[t, #], {t, tsamplings + zero}] &;
  NestWhile[iterate, xinit, Mean[Abs[# - #2]] > zero &, 2]
]

BTW, replacing NestWhile in the last step with NestWhileList, one can see datas generated in each iterative step.

Answer 2

There is no iteration in your code, and you're specifying the index of x as its variable, so the integrations inside the recursive formula will try to integrate over the index, which isn't correct. You could try the following:

x[0] = t;
h = 0.7;
Do[
    n = i;
    xs = x[n] /. t -> s;
    f = D[xs, {s, 2}] + xs^2 - s^4 - 2;
    x[n + 1] = x[n] + h*Integrate[s*(1 - t)*f, {s, 0, t}] + h*Integrate[t*(1 - s)*f, {s, t, 1}];
    Clear[n, xs, f];
, {i, 0, 7}]

You should expect that this might take some time, because the order of x and the number of terms increase exponentially with the order of 2, which also means that you're gonna need a very high numeric precision to compute properly. You can set the global precision by adding the following in the beginning:

$MinPrecision = 200;
$PreRead = (# /. s_String /; StringMatchQ[s, NumberString] && Precision@ToExpression@s == MachinePrecision :> s <> "`200." &);

For my PC, it took less than a second to get x[7], but for some reason x[8] (and higher) is taking forever (most likely due to precision overhead). Nevertheless, it yields the correct answer:

TableForm@Table[x[i] /. t -> 1/2, {i,0,7}]

---

UPDATE. If you prefer not to care about precision entirely and compute everything with infinite precision, then just define every number as rational form (such as h = 0.7 to h = 7/10). In such a case...