How to compute higher iterations in mathemtica

Question

I have the equation $u^{\prime\prime}(t)+u^{2}(t)-t^{4}-2=0$ such that $0\leq t\leq 1$and also I have $u(0)=0$ as well as $u(1)=1$. Noe the exact solution of the equation is $u(t)=t^{2}$. Now I want to compute the solution by the modified Mann method; \begin{equation*} x_{n+1}=x_{n}+h\int_{0}^{t}s(1-t)[x^{\prime\prime}_{n}(s)+x^{2}_{n}(s)-s^{4}-2]ds+h\int_{t}^{1}t(1-s)[x^{\prime\prime}_{n}(s)+x^{2}_{n}(s)-s^{4}-2]ds \end{equation*} with the starting value $x_{0}(t)=t$. If $t=0.5$ then the exact solution of the equation will be $u(t)=0.5^{2}=0.25$ and so the starting value will be $x_{0}(t)=t=0.5$. My code is

x[0] = t;
h = 0.7;
Do[n = i;
xs = x[n] /. t -> s;
f = D[xs, {s, 2}] + xs^2 - s^4 - 2;
x[(n + 1) _] := x[n + 1] = x[n] + h*Integrate[s*(1 - t)*f, {s, 0, t}] + h*Integrate[t*(1 - s)*f, {s, t, 1}];
Clear[n, xs, f];, {i, 0, 8}];
NumberForm[a1 = {Table[x[i] /. t -> (0.5), {i, 0, 7}]}, 5]

When I run my mathetica, I found a sequence of numbers as

0.5,0.33922,...,0.25005

Now for more than 9 iterations I see some error code. I also tried the following before my codes, but cant find the aim.

$MinPrecision = 200;
$PreRead = (# /. s_String /; StringMatchQ[s, NumberString] && Precision@ToExpression@s ==MachinePrecision :> s <> "`200." &);

I would be very thankfull If any one improve my code (or suggest a new code in new way) so that I find other iterations above 9,10,11, ... and so on.

Answer 1

The problem is that your expressions get exponentially large with increasing $n$. An efficient implementation with partial memoization:

h = 0.7;
Clear[x];
x[0] = Function[t, t];
x[n_Integer?Positive] := x[n] = Function[t, Evaluate[Expand[
  x[n - 1][t] + 
  hIntegrate[s(1-t)(x[n-1]''[s]+x[n-1][s]^2-s^4-2), {s, 0, t}] + 
  hIntegrate[t(1-s)(x[n-1]''[s]+x[n-1][s]^2-s^4-2), {s, t, 1}]]]]

Let's look at some results:

x[0][t]
(*    t    *)
x[1][t]
(*    0. + 0.335 t + 0.7 t^2 - 0.0583333 t^4 + 0.0233333 t^6    *)
x[2][t]
(*    0. + 0.110309 t + 0.91 t^2 - 0.0240465 t^4 - 0.016415 t^5 +
      0.0189 t^6 + 0.000651389 t^7 + 0.00102083 t^8 - 0.000151991 t^9 -
      0.00028054 t^10 + 0.000014436 t^12 - 2.0940210^-6 t^14    )

You can see that this is a polynomial in $t$ of order $2^{n+2}-2$. So for $n=9$ you'll have a polynomial of order 2046; is this what you want? If not, we could for example chop off all polynomial contributions that are smaller than a cutoff $\delta$:

h = 0.7;
δ = 10^-20;
Clear[x];
x[0] = Function[t, t];
x[n_Integer?Positive] := x[n] = Function[t, Evaluate[
  Chop[Expand[
    x[n-1][t] +
    h*Integrate[s(1-t)(x[n-1]''[s]+x[n-1][s]^2-s^4-2), {s, 0, t}] + 
    h*Integrate[t(1-s)(x[n-1]''[s]+x[n-1][s]^2-s^4-2), {s, t, 1}]],
  δ]]]

This is much faster:

Table[x[n][0.5], {n, 0, 20}]
(*    {0.5, 0.339219, 0.280943, 0.260626, 0.253639, 0.251246, 0.250427,
       0.250146, 0.25005, 0.250017, 0.250006, 0.250002, 0.250001,
       0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25, 0.25}    *)

Answer 2

This is a problem of basis functions choice to represent solution. The simplest basis in this case is {1,t,t^2,...,t^n} (Taylor series). We can restrict maximal power from the beginning as follows

nmax = 14; var = Table[t^n, {n, 0, nmax}];
h = 7/10; nn = 15; x[0] = t;
Do[
  xs[n] = x[n] /. t -> s;
  g[n] = D[xs[n], {s, 2}] + xs[n]^2 - s^4 - 2; 
  in1 = Integrate[s*g[n], s]; in2 = Integrate[g[n], s] - in1; 
  int1 = in1 /. s -> t; int2 = (in2 /. s -> 1) - (in2 /. s -> t);
  xn = x[n] + h*(1 - t) int1 + h*t int2; lst = CoefficientList[xn, t];
   x[n + 1] = 
   If[Length[lst] < Length[var], xn, Take[lst, Length[var]] . var];
  , {n, 0, nn}]; 

Solution in the point t=1/2

Table[N[x[i] /. t -> 1/2, 30], {i, 0, nn}]
{0.5, 0.33921875, 0.2809426617675349, 0.26062635193160333, 

0.2536391058021099, 0.25124579177605266, 0.25042664666458403, \ 0.2501461896648886, 0.25005010293913515, 0.25001715807367814, 

0.25000585393695235, 0.2500019724479996, 0.25000063876358225, \ 0.2500001802169856, 0.250000022466089, 0.24999996816592682}

Absolute error in the logarithmic scale

LogPlot[Abs[t^2 - x[nn]], {t, 0, 1}, 
 AxesLabel -> {"t", "Absolute error"}]

We also can solve this problem with zero absolute error using the Euler wavelets colocation method described in our paper and on my page as follows

eq = D[x[s], {s, 2}] + x[s]^2 - s^4 - 2 == 0; bc = {x[0] == 0, 
  x[1] == 1}; xs[t_] := t^2;
UE[m_, t_] := EulerE[m, t]
psi[k_, n_, m_, t_] := 
 Piecewise[{{2^(k/2) Sqrt[2/Pi] UE[m, 2^k t - 2 n + 1], (n - 1)/
      2^(k - 1) <= t < n/2^(k - 1)}, {0, True}}]
PsiE[k_, M_, t_] := 
 Flatten[Table[psi[k, n, m, t], {n, 1, 2^(k - 1)}, {m, 0, M - 1}]]
k0 = 3; M0 = 3; nn = 
 Total[With[{k = k0, M = M0}, 
   Flatten[Table[1, {n, 1, 2^(k - 1)}, {m, 0, M - 1}]]]]
dx = 1/(nn);  xl = Table[ l*dx, {l, 0, nn}]; tcol = 
 Table[(xl[[l - 1]] + xl[[l]])/2, {l, 2, nn + 1}]; Psijk = 
 With[{k = k0, M = M0}, PsiE[k, M, t1]]; Int1 = 
 With[{k = k0, M = M0}, Integrate[PsiE[k, M, t1], t1]];
Int2 = Integrate[Int1, t1]; Psi[y_] := Psijk /. t1 -> y; 
int1[y_] := Int1 /. t1 -> y; int2[y_] := Int2 /. t1 -> y;
M = nn; var = Array[v, {M}];
X2[t_] := var . Psi[t]; X1[t_] := var . int1[t] + v1; 
X[t_] := var . int2[t] + v1 t + v0;
eqn = Join[
  Table[X2[s] + X[s]^2 - s^4 - 2 == 0, {s, tcol}], {X[0] == 0, 
   X[1] == 1}]; varM = Join[{v0, v1}, var];
sol = FindRoot[eqn, Table[{varM[[i]], 1/10}, {i, Length[varM]}]] 

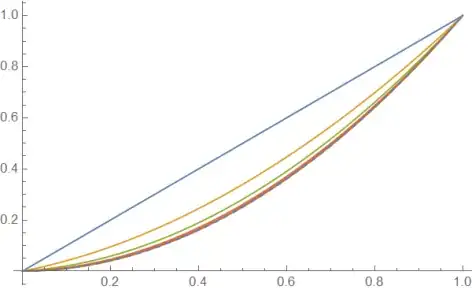
Visualization numerical solution and error

Show[Plot[xs[t], {t, 0, 1}], 
 ListPlot[Table[{t, X[t] /. sol}, {t, tcol}], PlotStyle -> Red]]
ListPlot[Table[xs[t] - X[t] /. sol, {t, tcol}], PlotStyle -> Red, 
 Filling -> Axis]

To decries error we use option

 sol1 = FindRoot[eqn, Table[{varM[[i]], 1/10}, {i, Length[varM]}], 
   WorkingPrecision -> 100];

Error of this solution is zero

Table[xs[t] - X[t] /. sol1, {t, tcol}]
Out[]= {0.10^-103, 0.10^-102, 0.10^-102, 0.10^-102, 0.10^-101, 
 0.10^-101, 0.10^-101, 0.10^-101, 0.10^-101, 0.10^-101, 
 0.10^-101, 0.10^-101}

Answer 3

Using NestListyou might optimize your code a bit. But you should be aware, that this iteration is symbolically (uses integrate) and creates very small numbers :

iterative function

iter[f_ (* pure function*)] := 
Block[{h = 0.7 (* optimaler Wert, Konvergenzgeschwindigkeit?*)}, 
Function[t,f[t] + h Integrate[s (1 - t) (f''[s] + f[s]^2 - s^4 - 2), {s, 0, t}] + h Integrate[t (1 - s) (f''[s] + f[s]^2 - s^4 - 2), {s, t, 1}] //Evaluate ]
]

iteration starting with x0[t]== t

sol = Map[#[t] &, NestList[iter, # &, 10]] // Quiet;

gives warning message: General::munfl: -1.4429910^-307+1.4265210^-307 is too small to represent as a normalized machine number; precision may be lost.

Plotshows good convergence

Show[Plot[sol , {t, 0, 1}], Plot[t^2, {t, 0, 1}, PlotStyle -> Dashed]]

Show[Plot[sol , {t, 0, 1}], Plot[t^2, {t, 0, 1}, PlotStyle -> Dashed]]