Plot various 2D curves in 3D

Question

I can embed a 2D curve f00==0 in 3D space using

zval=0
f00 = -3 (\[Pi]^6/64 + (-x^6 - y^6)) // ExpandAll // FullSimplify
curve = ContourPlot[f00 == 0, {x, -Pi, Pi}, {y, -Pi, Pi}];
XYcirc = Cases[Normal@curve, Line[x_] :> x, Infinity];
Zcirc = Table[zval, {i, Dimensions[XYcirc][[2]]}];
Xcirc = Flatten@XYcirc[[All, All, 1]];
Ycirc = Flatten@XYcirc[[All, All, 2]];
XYZcirc = Transpose[{Xcirc, Ycirc, Zcirc}];
g4 = ListLinePlot3D[XYZcirc, PlotStyle -> Directive[red, Opacity[0.65]], Mesh -> False, PlotRange -> All]

where I have extracted $x,y$ coordinates from f00==0 and set the $z$ coordinate to z=zval. Based on the answer to one of my recent quesions, I can now generate disconnected curves. For instance, setting f1==0 or f2==0 with

f1 = -3 (x^6 + y^6 + z^6) + 5 (x^4 + y^4 + z^4) \[Pi]^2 -  5/9 (x^2 + y^2 + z^2) \[Pi]^4 + \[Pi]^6/81 /. {z -> zval}
f2 = -6 (x^5 + y^5 + z^5) \[Pi] + 20/9 (x^3 + y^3 + z^3) \[Pi]^3 -  2/27 (x + y + z) \[Pi]^5 /. {z -> zval}

gives multiple points. To obtain the coordinates of these points, I have tried the script above for the f1==0 and f2==0 functions, but I get many errors such as

"Part 2 of {23} does not exist."

I have also tried to replace Dimensions[XYcirc] with Dimensions[XYcirc[[1]]], but this also didn't help.

Do you have any suggestions on how to extract these points and plot them in a 3D plot?

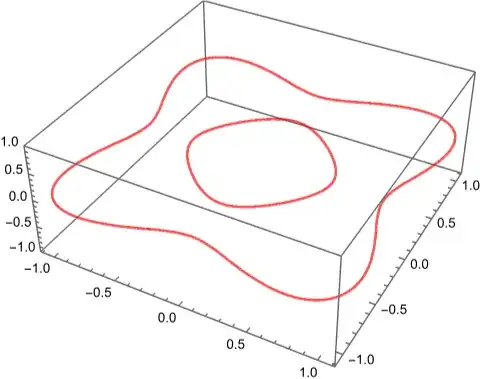
Please show what you tried: f1==0 gives some surfaces in 3D (not a list {x,y}) — Ulrich Neumann, Jun 13 '22 at 13:54
f1=\[Pi]^6/81 - 5/9 \[Pi]^4 (x^2 + y^2) + 5 \[Pi]^2 (x^4 + y^4) - 3 (x^6 + y^6) is a function of $(x,y)$ as I set z=zval. Then plot curve = ContourPlot[f1 == 0, {x, -Pi, Pi}, {y, -Pi, Pi}] and the rest follows from the first script above. — Shasa, Jun 13 '22 at 13:58
ContourPlot3D[f1 == 0, {x, -Pi, Pi}, {y, -Pi, Pi}, {z, -Pi, Pi}, MeshFunctions -> {Function[{x, y, z}, z]}, Mesh -> {{-.3, -.3, -.1, 0.1, .2, .3}}, PlotPoints -> 100, PlotRange -> All, ContourStyle -> None, BoundaryStyle -> None, Boxed -> False]? — cvgmt, Jun 13 '22 at 14:14
@Shasa Thank you, I got it. ContourPlot[f1 == 0,...] gives two curves, that might cause the errors! — Ulrich Neumann, Jun 13 '22 at 14:15
@Ulrich-Neumann Exactly! And I don't know how to extract data from these disconnected curves. — Shasa, Jun 13 '22 at 14:18
@cvgmat This is great and partially solves my problem! I also want to extract these points from the ContourPlot3D? Something like Xcirc and Ycirc above. Do you have any suggestions? — Shasa, Jun 13 '22 at 14:21
@Shasa Cases[Normal@curve, Line[x_] :> x, Infinity] gives a list of two(!) curves, you have to pick them separately! — Ulrich Neumann, Jun 13 '22 at 14:21
@UlrichNeumann Could you give a hint on how to separate them? — Shasa, Jun 13 '22 at 14:23
@hasa lists=Cases[Normal@curve, Line[x_] :> x, Infinity] . First list: lists[[1]], ... — Ulrich Neumann, Jun 13 '22 at 14:27
@UlrichNeumann By using Dimensions[XYcirc[[1]]] in my question, I also tried to get the correct dimension, but somehow it didn't work. — Shasa, Jun 13 '22 at 14:31

score 7 · Accepted Answer · answered Jun 13 '22 at 14:25

7

Here's a slightly simpler approach that works even when there is more than one contour, generated using your $f_1$ expression:

curvef1 = ContourPlot[f1 == 0, {x, -Pi, Pi}, {y, -Pi, Pi}];
points3D = 
  Cases[Normal@curvef1, Line[x_] :> x, Infinity] /. 
     {x_?NumericQ, y_?NumericQ} :> {x, y, zval};
ListLinePlot3D[
  points3D, 
  PlotStyle -> Directive[Red, Opacity[0.65]], 
  PlotRange -> All
]

answered Jun 13 '22 at 14:25

MarcoB

67,153
18
91
189

Thanks! This script generates both coordinates and the final plot. – Shasa Jun 13 '22 at 14:37

score 5 · Answer 2 · answered Jun 13 '22 at 17:42

Marco's answer would be the best thing to do in this particular case. An alternative that is sometimes done is to use the MeshFunctions option of ContourPlot3D[]:

With[{zval = 0}, 
     {ContourPlot3D[-3 (x^6 + y^6 + z^6) + 5 (x^4 + y^4 + z^4) π^2 -
                    5/9 (x^2 + y^2 + z^2) π^4 + π^6/81 == 0,
                    {x, -π, π}, {y, -π, π}, {z, -1, 1}, 
                    BoundaryStyle -> None, BoxRatios -> Automatic, 
                    ContourStyle -> None, Mesh -> {{zval}}, MeshFunctions -> {#3 &}, 
                    MeshStyle -> Directive[Red, Opacity[0.65]], PlotPoints -> 25], 
      ContourPlot3D[-6 (x^5 + y^5 + z^5) π + 20/9 (x^3 + y^3 + z^3) π^3 -
                    2/27 (x + y + z) π^5 == 0,
                    {x, -π, π}, {y, -π, π}, {z, -1, 1}, 
                    BoundaryStyle -> None, BoxRatios -> Automatic, 
                    ContourStyle -> None, Mesh -> {{zval}}, MeshFunctions -> {#3 &}, 
                    MeshStyle -> Directive[Red, Opacity[0.65]], PlotPoints -> 25]} //
      GraphicsRow]

contours

A similar answer has been suggested by @cvgmt in the comments above. — Shasa, Jun 14 '22 at 06:14

Plot various 2D curves in 3D

2 Answers2

Linked