I have a complex function given by
f1 = Sqrt[-16 x^4 - 16 y^4 - 16 z^4 - 32 I x^3 \[Pi] + 24 x^2 \[Pi]^2 + 8 I x \[Pi]^3 - \[Pi]^4]
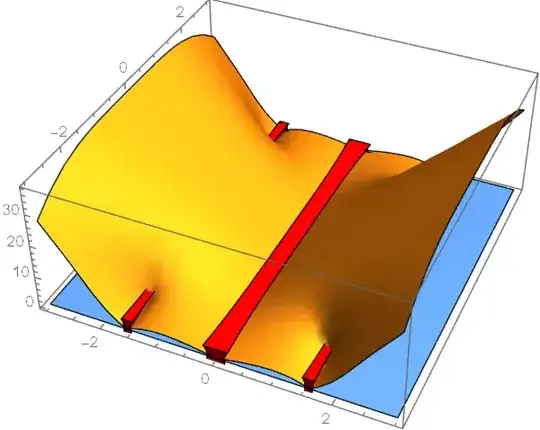
When I plot the real part of this function using
Plot3D[{Re@f1 /. {z -> 0}, 0}, {x, -3, 3}, {y, -3, 3}]
I see that there are $(x,y)$ at which Re[f1]==0. However, when I try to plot these points separately using
ContourPlot3D[Re@f1 == 0, {x, -3, 3}, {y, -3, 3}, {z, -3, 3}, MeshFunctions -> {#3 &}, Mesh -> {{0}}, PlotPoints -> 100, PlotRange -> All, ContourStyle -> None, BoundaryStyle -> None, Boxed -> False]
The output is empty!
I have checked these threads and also these ones but couldn't figure out why the ContourPlot3D does not generate the correct results.
Do you have any suggestions?

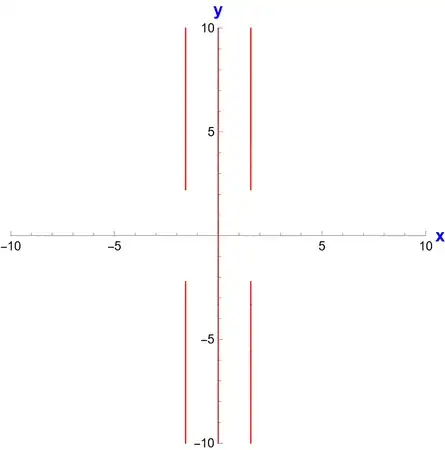

z==0, Contourplot cannot detect these kind of contours! – Ulrich Neumann Jun 14 '22 at 07:48