1

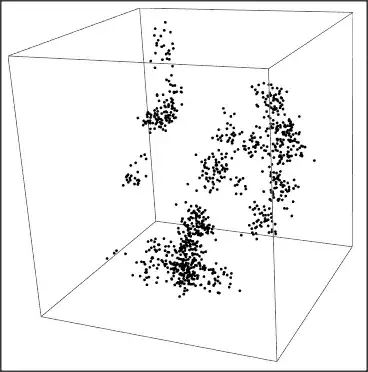
I would like to build a simple visualization of the distribution of galaxies on a large scale model of the universe. Currently, my galaxies are represented as uniform random black dots in a 3D cube, using the minimal working code below (this is a manipulate box, to see the effect of adding random dots, from 1 to 1000):

r = 1;

box = Graphics3D[{Opacity[0.1], EdgeForm[Gray], Cuboid[{0, 0, 0}, {1, 1, 1}]}];


x0[n_, r_] := x0[n, r] = RandomReal[{0, 1}]
y0[n_, r_] := y0[n, r] = RandomReal[{0, 1}]
z0[n_, r_] := z0[n, r] = RandomReal[{0, 1}]


particles[n_, r_] := Graphics3D[{PointSize -> 0.005,
    Point[{x0[n, r], y0[n, r], z0[n, r]}]
}]


graph3D[Np_, r_] := Show[
    {box, Table[{particles[n, r]}, {n, 1, Np}]},
    PlotRange -> {{0, 1}, {0, 1}, {0, 1}},
    ImageSize -> {700, 700},
    SphericalRegion -> True,
    Method -> {"RotationControl" -> "Globe"}
]


Manipulate[graph3D[Np, r], {{Np, 1, "N"}, 1, 1000, 1}, Row[{Button["Randomiser", {r = RandomReal[]}]}]]

I want to modify the random distribution to add correlation between galaxies, so the dots are creating random clusters and filaments as seen in the popular 3D simulations found on the internet (see for example this one: https://hipacc.ucsc.edu/Bolshoi/index.html).

So how could we modify the three functions x0[n_, r_], y0[n_, r_], z0[n_, r_] to introduce some random correlations between the black dots (i.e to create clusters and random structures)?

Please, I'm looking for something very simple, nothing fancy or complicated, that could work with an old version of Mathematica. I don't need something very realistic and I don't want to reproduce the large Newtonian N-body simulations like the Millenium Run! I simply want to produce a 3D visualization that feels qualitatively similar to the cosmic web:

enter image description here

Cham
  • 4,093
  • 21
  • 36
  • My suggestion would be to research methods for generating random fractals. For example, the diamond-square algorithm that's used for generating landscapes could probably be re-purposed (in some fashion) to create 3D "landscapes". I think it'll be much easier to seed some initial conditions from which you generate a fractal iteratively than to define probability distributions. – lericr Jul 25 '22 at 19:01
  • 2
    "something very simple, nothing fancy or complicated" - well, you're not asking for something very simple though. I agree that modifying the distributions seems like a dead end. Daniel's approach below is much more promising. – MarcoB Jul 25 '22 at 19:14
  • This question is likely of interest, especially the accepted answer with a modification on Simon Wood's post – George Varnavides Jul 25 '22 at 20:56

1 Answers1

6

Here is a simple first approach:

We seed our "universe" by some random mass points (aka dark matter). Then the next mass point is chosen by an empirical distribution consisting of the already created mass points plus some noise. Then we repeat:

noise = 0.1;
dat = RandomReal[{-1, 1}, {20, 3}];
Do[AppendTo[dat, 
  noise RandomReal[{-1, 1}, 3] + 
   RandomVariate[EmpiricalDistribution[dat]]], 1000]
Graphics3D[Point[dat]]

enter image description here

Addendum

To create a "Manipulate", we may e.g. write:

getPts[n_, noise_] := Module[{dat = RandomReal[{-1, 1}, {20, 3}]},
  Do[AppendTo[dat, noise RandomReal[{-1, 1}, 3] + RandomChoice[dat]], 
   n]; dat]
Manipulate[
 Graphics3D[Point[getPts[n, noise]], 
  PlotRange -> {{-1, 1}, {-1, 1}, {-1, 1}}]
 , {{noise, 0.1}, 0, 0.4}, {{n, 1000}, 100, 5000}]
Daniel Huber
  • 51,463
  • 1
  • 23
  • 57
  • Seems great. Unfortunately, my very old version of Mma (7.0) doesn't recognize the commands RandomVariate and EmpiricalDistribution. Are there equivalent commands that would work for old versions of Mma? – Cham Jul 25 '22 at 20:05
  • 3
    RandomVariate[EmpiricalDistribution[dat]] simply selects a random point from the current dataset, so you can replace that with RandomChoice[dat] (which seems to have been introduced in v6.0) – George Varnavides Jul 25 '22 at 20:54
  • @GeorgeVarnavides, works like a charm! Thanks! I'll wait a bit before marking this answer, since others may suggest other solutions. – Cham Jul 25 '22 at 23:33
  • How do you make this thing a manipulate box, with the noise parameter and the number of particles as the sliders variables (see my MWE in the question)? – Cham Jul 27 '22 at 14:01
  • 1
    Look at the addition to my answer. – Daniel Huber Jul 27 '22 at 16:45
  • Thanks! It's working great! – Cham Jul 27 '22 at 17:05
  • Is it possible to render the points as blurry disks? Adding some transparent color to the Graphics3D[point[dat]] directive helps a bit (for example: RGBColor[{0,5,0.4,1.0,0.4}], PointSize -> 0.004), but a blurry disk would be much better for the output. – Cham Jul 28 '22 at 01:13
  • Simply apply "Blur" to the whole Graphics. – Daniel Huber Jul 28 '22 at 07:42
  • Make 2 graphics, the one that you want to blur and the rest. Then join them using "Show" – Daniel Huber Jul 28 '22 at 14:44
  • Daniel, it doesn't work. The version that is blurred can't be rotated anymore. – Cham Jul 28 '22 at 14:50
  • Blur is the last step, rotate first. – Daniel Huber Jul 28 '22 at 15:51
  • Rotate first? => rotate the part to be blurred and then blur it. – Daniel Huber Jul 28 '22 at 18:18
  • @DanielHuber, as a refinement to your method, how do you make variable (i.e random) point size for each particle, and also variable colors? – Cham Jul 28 '22 at 23:41
  • Look at "PointSize" and color can be specified in "Graphics". To restrict color to some element, enclose it in braces. – Daniel Huber Jul 29 '22 at 07:36
  • 1
    It will work if you write PointSize[...] instead of PointSize->.... – Daniel Huber Jul 29 '22 at 13:09
  • Try: getPts[n_, noise_] := Module[{dat = RandomReal[{-1, 1}, {20, 3}]}, Do[AppendTo[dat, noise RandomReal[{-1, 1}, 3] + RandomChoice[dat]], n]; {PointSize[RandomReal[{0.003, 0.006}]], Point[#]} & /@ dat] Manipulate[ Graphics3D[getPts[n, noise], PlotRange -> {{-1, 1}, {-1, 1}, {-1, 1}}], {{noise, 0.1}, 0, 0.4}, {{n, 1000}, 100, 5000}] – Daniel Huber Jul 29 '22 at 13:20
  • The point is, you must evaluate "PointSize" separately for every point. – Daniel Huber Jul 29 '22 at 16:05