How to get fuzzy points in a 3D view?

Question

I would like to produce fuzzy random points (sprites like) in a 3D view. Applying a Blur command doesn't do the trick since the view is then frozen and we couldn't rotate the view anymore, and I don't want to blur the frame box too.

Here's a MWE to play with (currently, I'm using some transparency to blur slightly the particles, but the effect isn't that good!) :

particles := RandomReal[{-1, 1}, {1000, 3}]
graph := Graphics3D[{RGBColor[{0.5, 0.4, 1.0, 0.4}], PointSize -> 0.006, Point[particles]}]
Show[graph,
    PlotRange -> {{-1, 1}, {-1, 1}, {-1, 1}},
    Boxed -> True,
    Ticks -> None,
    Background -> Black,
    ImageSize -> {700, 700},
    SphericalRegion -> True,
    Method -> {"RotationControl" -> "Globe"}
]

So the question is simple: Is there a way to get fuzzy dots/points without applying a Blur command to the whole thing, in a way that the view could still be rotated? Ideally, the solution (if any) should be applicable to an old version of Mathematica (I'm still using Mma 7.0, until I upgrade the whole computer!).

Maybe the solution is to use a sprite PNG image for each particle, but then that small picture should stay oriented front to the viewer, whatever what he do with the view. I doubt that this would work well for an output that draws several thousands of particles, and it may be way too long to program just to get fuzzy dots in a manipulate box.

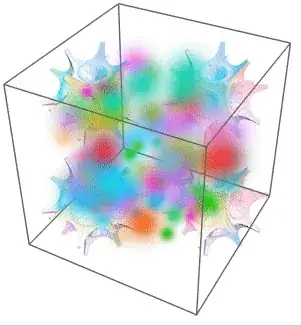
EDIT:. The fuzzy sprite-like particles I would like to get are looking like this:

A single particle, without any specific color:

Several particles, each one using the same disk blob (or sprite), but using different colors and sizes:

Answer 1

As OP already suggested, an image sprite based approach could be a solution, except a special rendering option "3DRenderingMethod" -> "BSPTreeOrDepthBuffer" is needed in order to give a correct result. (Note however this solution doesn't really work in 13.1, at least the Windows version, due to unsettled z-fighting.)

$Version
(* 13.0.1 for Microsoft Windows (64-bit) (January 28, 2022) *)
spriteAlpha = With[{r = 20}
      , GaussianMatrix[{r, r/3}] // Rescale // Chop // Image
    ]

The sprites can be inserted in Graphics3D using Inset (or if multiple copies of the same sprite is needed, we could use one Inset coupled with a Translate[g, {pos1, pos2, ...}]):

graph = Module[{n = 100}
  , MapThread[
          Function[{col, pos, size, maxOpacity}
               , ConstantImage[col, ImageDimensions@spriteAlpha, ImageSize -> size] //
               SetAlphaChannel[#, maxOpacity spriteAlpha] & //
               Inset[#, pos] &
           ], {
          RandomColor[LABColor[.7, _, _], n]
          , RandomPoint[Ball[{0, 0, 0}, 1], n]
          , RandomInteger[{10, 50}, n]
          , RandomReal[{.3, 1}, n]
      }] //
 Graphics3D[#
    , PlotRange -> {{-1, 1}, {-1, 1}, {-1, 1}}
    , SphericalRegion -> True, RotationAction -> "Clip"
    , ImageSize -> 200] & //
 Style[#, RenderingOptions -> {
     (*"DepthPeelingLayers" -> 64,*)
     "3DRenderingMethod" -> "BSPTreeOrDepthBuffer"
     }] &
]

It looks like this approach performs good enough on my computer. At least n = 1000 doesn't really slow down the 3D interaction. "DepthPeelingLayers" could use a larger value than the default 8 in case of really lots of sprites.

GIFs to demonstrate the 3D graphic is really transparent, also the performance on Windows: