I have a function $f(u,v)$ on some domain of $(u,v)$ and would like to find (numerically) the set of couples* $(u_0,v_0)$ s.t. $f(u_0,v_0)=0$, for instance (just and example to illustrate, in practice I will use arbitrary non analytical functions)
ContourPlot[BesselJ[3, Sin[u^2 - v]] == 0, {u, -1, 1}, {v, -1, 1}]
FindRoot does not work immediately because it needs two equations. Any easy implementation for this problem ?
*"the set of couples" has naturally infinite elements, so I would expect a set of finitely countable elements with adjustable density.


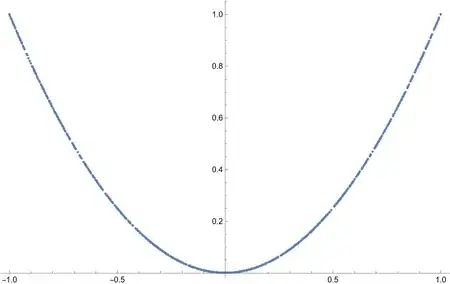



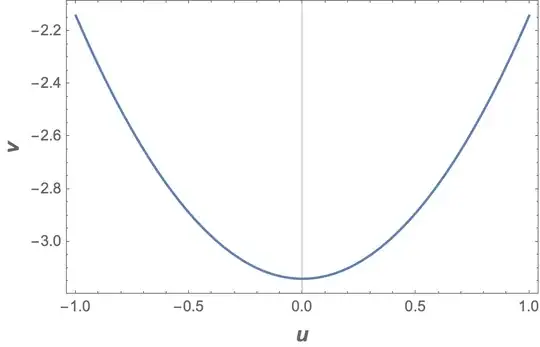
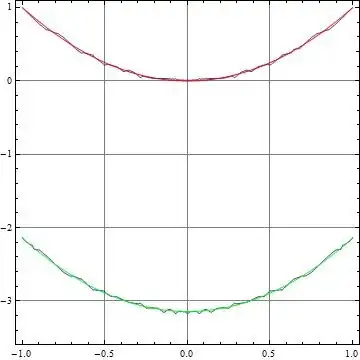
ContourPlot[...,PlotPoints->100]. – user293787 Jul 28 '22 at 13:16