Detect an event in NDSolve that is initially true

Question

I want to check at what time the derivative of a function converges to zero. If the function starts far from equilibrium, the event is detected correctly at t=7.55822:

NDSolveValue[{x'[t] == -.9 x[t], x[0] == 1, 
   WhenEvent[Abs[x'[t]] <= 10^-3, Echo@{"FOUND at", t}; "StopIntegration"]
   }, x, {t, 0, 20}] // ListLinePlot
(* {FOUND at,7.55822} *)

However, I have no means to check generally within WhenEvent whether the test is initially true. Consequently, no event is triggered in the next example. Note, that I have tried to add a composite condition, dependent on time as well.

NDSolveValue[{x'[t] == 0, x[0] == 1, 
   WhenEvent[Abs[x'[t]] <= 10^-3 && t >= 0, Echo@{"FOUND at", t}; "StopIntegration"]
   }, x, {t, 0, 20}] // ListLinePlot

Moreover, if I change the order of conditions from Abs[x'[t]] <= 10^-3 && t >= 0 to t >= 0 && Abs[x'[t]] <= 10^-3, I get the following error messages:

NDSolveValue::nbnum1: "The function value Abs[0&]<=1/1000
is not True or False when the arguments are {0.,1.}."

How can one generally check that the condition is true initially when no crossing is detected by the integrator?

Answer 1

Update: Clarified when an event may depend on the highest-order derivative. Thanks to @Chris K for pointing out an exception to the original characterization.

I think the practical answer to the main question is to test whether the condition is true initially "initially", that is, before one calls NDSolve[].

However, I would like to respond to the observation in the OP of the effect of changing the order in And[] of the event. Maybe there's a better place to post this way to inspect an event as it is constructed by NDSolve[], but I didn't find one. I know the question of changing the order has come up before, though.

An event of the form evt && cond is parse in a special way. The first argument is processed as an event, that is, equations and inequalities are converted to a numeric function whose sign change in a step from t == t1 to t == t2 indicates an event has occurred. The second argument represent a boolean condition: if true at an event, then the event action is taken. It appears there is a restriction on the condition. It may depend only the highest-order derivative if either the derivative appears in evt or the option setting Method -> {"EquationSimplification" -> "Residual"} is used. (Normally in an explicit ODE $Y' = F(t, Y)$, the derivatives $Y'$ are not considered "state variables." In an implicit ODE $F(t,Y,Y')=0$, which is what "EquationSimplification" -> "Residual" enforces, the derivatives $Y'$ treated as state variables. At least that's how I keep the difference in mind, plus maybe it's more efficient to have events depend on fewer variables.)

If the form of the event is not of the form evt && cond, or if evt is not of one of the forms given in the table of example event forms in the documentation for WhenEvent[], then the whole event is treated as a boolean function and an event is indicated by its changing from False to True (only).

{state1} = NDSolve`ProcessEquations[{x'[t] == 0, x[0] == 1,
    WhenEvent[Abs[x'[t]] == 10^-3 && t >= 0 , Echo@{"FOUND at", t}; 
     "StopIntegration"]},
   x, {t, 0, 20}];
{state2} = 
  NDSolve`ProcessEquations[{x'[t] == 0, x[0] == 1, 
    WhenEvent[t >= 0 && Abs[x'[t]] <= 10^-3, Echo@{"FOUND at", t}; 
     "StopIntegration"]}, x, {t, 0, 20}];
{state3} = 
  NDSolve`ProcessEquations[{x'[t] == 0, x[0] == 1, 
    WhenEvent[t >= 0 && Abs[x'[t]] <= 10^-3, Echo@{"FOUND at", t}; 
     "StopIntegration"]}, x, {t, 0, 20}, 
   Method -> {"EquationSimplification" -> "Residual"}];

The state data object has two lists of NDSolve`EventData[], one for the backward integration direction and one for the forward one. Initially they are the same, so we'll examine just one for each state.

state1["Events"]
SameQ @@ %

evt1 = state1["Events"][[2, 1]];
evt2 = state2["Events"][[2, 1]];
evt3 = state3["Events"][[2, 1]];

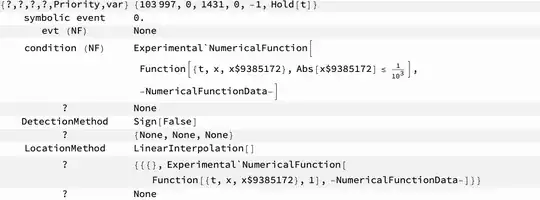
The following shows the structure of the NDSolve`EventData[] for each ODE, at least as much as I have been able to discover. Note the difference in the condition in the 2nd and 3rd ODEs. Depending on the method of equation simplification, in the condition, the x'[t] is replaced by a numerical function argument or left as constant parameter of the numerical function. Note also that the evt, namely, t >= 0, has be simplified to True (presumably because the interval of integration is 0 <= t <= 20}).

(* formatters *)
headers = {"{?,?,?,?,Priority,var}", "symbolic event", "evt (NF)", 
   "condition (NF)", "?", "DetectionMethod", "?", "LocationMethod", 
   "?", "?"};
gridform = 
  Grid[Transpose@{headers, #}, Alignment -> {{Center, Left}}(*,
    Dividers->All*), 
    Background -> {None, {{GrayLevel[0.95], GrayLevel[0.99]}}}] &;

---

List @@ evt1 // gridform

---

List @@ evt2 // gridform

---

List @@ evt3 // gridform

---

Thanks to @xzczd for these references to related Q&A:

• Inconsistent behavior of WhenEvent[ ]
• Options of WhenEvent

Answer 2

This post is to answer the first question, complementing Micheal E2's answer: How to test initially, outside of NDSolve, if an event condition is true?

I think my solution is not very general, and there is probably better way. Set up a 2D dynamical system with an event condition test that is defined outside of WhenEvent. It tests if the sum of derivatives is close to zero:

eq = {x'[t] == x[t] - x[t]^2, y'[t] == y[t] - x[t] y[t]};
init = {x[0] == .01, y[0] == .02};
test = Abs[x'[t]] + Abs[y'[t]] <= 10^-3;
event = WhenEvent["test", Echo@{"FOUND at", t}; "StopIntegration"] /. "test" -> test;
ListLinePlot@NDSolveValue[{eq, init, event}, {x, y}, {t, 0, 100}]
(* {FOUND at,12.6008} *)

The event is correctly detected, but note how test had to be manually injected into WhenEvent due to its HoldAll property.

Let's start the system from equilibrium, and perform the initial testing. Note, that WhenEvent does not fire during NDSolve, but the initial test returns True, correctly capturing the equilibrium (in this case there might not be need to numerically integrate the system at all).

init = {x[0] == 1, y[0] == 2};
test /. Rule @@@ eq /. t -> 0 /. Rule @@@ init
NDSolveValue[{eq, init, event}, {x, y}, {t, 0, 100}] // ListLinePlot
(* True *)

My issue with my approach is that it relies on multiple factors that would be unnecessary had NDSolve done a precheck:

1. The test that must be defined outside of WhenEvent so that it can be used both in the pre-test and by NDSolve.
2. Dynamical equations and initial conditions must be provided separately for the replacement to work.
3. Non-well-formed equations (e.g. where the derivative is on the right side) may not be as easily converted to rules for pre-testing.

I find this solution far from elegant, and probably prone to not work in corner cases, but is a proof of principle. Is there a better way?