Consider the following simple example:
sol = NDSolve[ {x''[t] == 1, x'[0] == 0, x[0] == 0,
WhenEvent[Abs[x[t]] > 1 && x[t] > 2, {x'[t] -> -3 x'[t]}]},
x[t], {t, 0, 4}];
Plot[x[t] /. sol[[1]], {t, 0, 4}]

Clearly WhenEvent[] is missing the x[t] > 2 occurrence. This may happens (my interpretation) if the event detection routine checks for the occurrence of the first part of the AND clause and then for the other AND components, instead of checking them as an OR event trigger.
As the Abs[x[t]] > 1 event isn't fired again between 1 and 2, the rest of the AND clause doesn't get tested again.
In testing this interpretation, we can reverse the clause:
sol = NDSolve[{x''[t] == 1, x'[0] == 0, x[0] == 0,
WhenEvent[x[t] > 2 && Abs[x[t]] > 1, {x'[t] -> -3 x'[t]}]},
x[t], {t, 0, 4}];
Plot[x[t] /. sol[[1]], {t, 0, 4}]
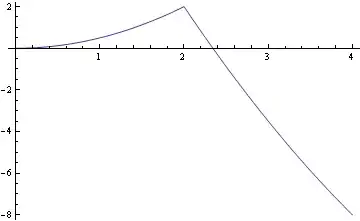
which now works as expected. Of course this isn't a proof.
But the strange thing is that reverting to the first version, but encapsulating the clause in a function, also works as expected:
clause[p_] := Abs[p] > 1 && p > 2
sol = NDSolve[{x''[t] == 1, x'[0] == 0, x[0] == 0,
WhenEvent[clause[x[t]], {x'[t] -> -3 x'[t]}]}, x[t], {t, 0, 4}];
Plot[x[t] /. sol[[1]], {t, 0, 4}]
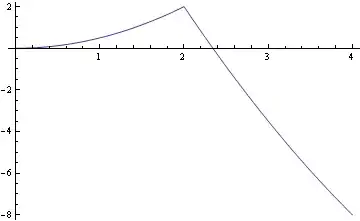
So, what is the moral? Always put your WhenEvent[] clause as a function?
WhenEvent[Null;Abs[x[t]]>1&&x[t]>2,{x'[t]->-3x'[t]}].. – Silvia Dec 24 '13 at 18:28WhenEvent[ ]thing isn't mature enough – Dr. belisarius Dec 24 '13 at 19:25