Finding inverse of an algebraic function and using ListLinePlot

Question

I am trying to find the Plot of Temperature v/s Free energy, for which I am using this code:


Ft[rpt_] = (3*Qt^2 + rpt^2 - rpt^4)/
   (4*rpt);
Tt[rpt_] = (1 - Qt^2/rpt^2 + 
    3*rpt^2)/(4*Pi*rpt);
rpt[Tt_] = Simplify[PowerExpand[
      SolveValues[Tt[rpt] == Tt, 
       rpt]]][[1]];
Ft[Tt_] = Ft[rpt] /. rpt -> 
     rpt[Tt]; 
Block[{Qt = 0.11}, ListLinePlot[
   Table[{Tt, Ft[Tt]}, {Tt, 0.05, 
     0.5, 0.01}]]]

I am just getting a straight line instead of the expected plot. Did I make a mistake while finding the inverse of the above given algebraic function?

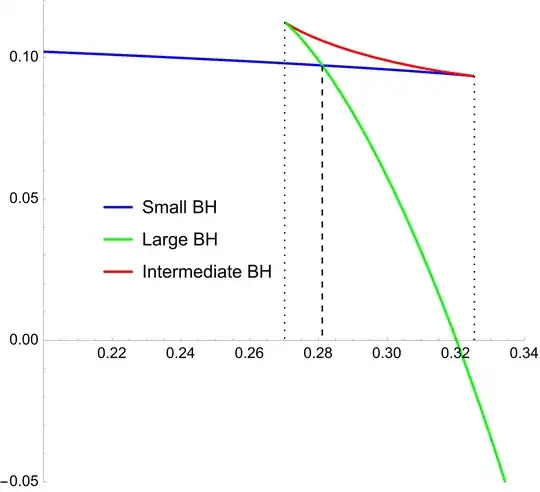
Try Block[{Qt = 11/100}, Plot[Ft[x], {x, 1/1000, 10}, WorkingPrecision -> 16] ] — Michael E2, Sep 03 '22 at 18:15
@MichaelE2 It's on page 5 of this paper -> https://arxiv.org/pdf/2205.02122.pdf — codebpr, Sep 03 '22 at 18:15
I am not getting a straight line now but the plot is incorrect. Maybe I have made a mistake in the code and there is a bug. — codebpr, Sep 03 '22 at 18:19
According to the paper Ft[0.2]/.Qt->0.11 should give approx 0.1. However, your function gives approx. -0.1. Therefore, there seems to be something amiss with your function Ft. — Daniel Huber, Sep 03 '22 at 19:25

Bob Hanlon · Accepted Answer · 2022-09-03T20:29:18.960

Clear["Global`*"]

Ft[rpt_] = (3*Qt^2 + rpt^2 - rpt^4)/(4*rpt);

Tt[rpt_] = (1 - Qt^2/rpt^2 + 3*rpt^2)/(4*Pi*rpt);

Qt = 11/100;

(tp1 = {#[[1]], Ft[rpt1 = (rpt /. #[[2]])]} &@
     Maximize[{Tt[rpt], 1/16 < rpt < 1}, rpt] // FullSimplify) // N

(* {0.325369, 0.0933627} *)

(tp2 = {#[[1]], Ft[rpt2 = (rpt /. #[[2]])]} &@
     Minimize[{Tt[rpt], rpt1 < rpt < 1}, rpt] //
    FullSimplify) // N

(* {0.270166, 0.11244} *)

You can use ParametricPlot to plot the implicit relation.

pplt = ParametricPlot[{Tt[rpt], Ft[rpt]},
   {rpt, 1/16, 1.2},
   PlotRange -> {{0.2, 0.34}, {-0.05, 0.12}},
   AspectRatio -> 1,
   ColorFunction -> Function[{Tt, Ft, rpt},
     If[rpt <= rpt1, Blue, If[rpt <= rpt2, Red, Green]]],
   ColorFunctionScaling -> False];
ip = GraphicsMeshFindIntersections[pplt][[1]]
(* {0.281118, 0.0971422} *)
Legended[
 Show[
  pplt,
  Graphics[
   {Black, Dashed, Line[{ip, {ip[[1]], 0}}],
    Dotted, Line[{tp1, {tp1[[1]], 0}}],
    Line[{tp2, {tp2[[1]], 0}}]}],
  PlotRange -> {{0.2, 0.34}, {-0.05, 0.12}},
  AxesOrigin -> {0.2, 0}],
 Placed[
  LineLegend[{Blue, Green, Red},
   {"Small BH", "Large BH", "Intermediate BH"}],
  {.3, .5}]]

Finding inverse of an algebraic function and using ListLinePlot

1 Answers1

Linked