Solving 3D Nonlinear Integral Partial Differential Equation

Question

I am trying to solve Equation number (1.2) numerically in MATHEMATICA. This equation is solved in the papers https://arxiv.org/pdf/2205.05193.pdf, https://arxiv.org/pdf/2202.13264.pdf, and https://arxiv.org/pdf/2005.05718.pdf. This equation is quite similar to I am trying to solve nonlinear Schrödinger equation with dipolar interaction which @AlexTrounev solved. I like to find the figures posted below and energy especially kinetic and dipolar energy. This paper might be a little help https://arxiv.org/pdf/1506.03283.pdf as Equation number (1.3) goes to infinity at the center.

Here I paste my failed attempt to modify the code from @AlexTrounev

Needs["NumericalDifferentialEquationAnalysis`"];
np = 4; xg = GaussianQuadratureWeights[np, -L, L]; xpoints = 
 xg[[All, 1]];
xweights = xg[[All, 2]];
yg = GaussianQuadratureWeights[np, -L, L]; ypoints = yg[[All, 1]];
yweights = yg[[All, 2]];
zg = GaussianQuadratureWeights[np, -L, L]; zpoints = zg[[All, 1]];
zweights = zg[[All, 2]];
sol[0][x_, y_, z_, t_] := 
  E^(- (x^2 + y^2 + z^2)/2);
[Omega]x = 45; [Omega]y = 45; [Omega]z = 133; gmean[Omega] = (

[Omega]x [Omega]y [Omega]z)^(
 1/3); [Gamma] = [Omega]x/gmean[Omega]; [Lambda] = 

[Omega]y/gmean[Omega]; [Nu] = [Omega]z/gmean[Omega];
a0 = 5.29*10^-5; a = 85 a0; add = 131 a0; [Epsilon]dd = add/a;
[Gamma]QF = 
 128/3 Sqrt[[Pi] a^5] (1 + 1.5 [Epsilon]dd^2); angle = ((
  3 Cos[[Phi]]^2 - 1)/2); [Phi] = 0;
Nat = 10^6; L = 10; dt = 1/100; nt = 100; T = 
 Table[i dt, {i, 0, 1001}];
nkx[0] = Table[
   Sum[xweights[[i]] Exp[
      I xpoints[[j]] xpoints[[i]]] Abs[
       sol[0][xpoints[[i]], 0, 0, 0]]^2, {i, Length[xg]}], {j, 
    Length[xg]}];
nky[0] = Table[
   Sum[yweights[[i]] Exp[
      I ypoints[[j]] ypoints[[i]]] Abs[
       sol[0][0, ypoints[[i]], 0, 0]]^2, {i, Length[yg]}], {j, 
    Length[yg]}];
nkz[0] = Table[
   Sum[zweights[[i]] Exp[
      I zpoints[[j]] zpoints[[i]]] Abs[
       sol[0][0, 0, zpoints[[i]], 0]]^2, {i, Length[zg]}], {j, 
    Length[zg]}];
finalnk[0] = nkx[0] nky[0] nkz[0];
intn[0] = 
  1/(6 [Pi]^2)
    angle Table[{xpoints[[j]], ypoints[[k]], zpoints[[m]], 
     Re[Sum[xweights[[j]] yweights[[k]] zweights[[
         m]] Exp[-I xpoints[[j]] xpoints[[i]]]  Exp[-I ypoints[[
           k]] ypoints[[i]]]  Exp[-I zpoints[[m]] zpoints[[i]]] ((
          3 zpoints[[m]]^2)/(
          xpoints[[j]]^2 + ypoints[[k]]^2 + zpoints[[m]]^2) - 
          1) finalnk[0][[i]], {i, Length[xg]}]]}, {j, Length[xg]}, {k,
      Length[yg]}, {m, Length[zg]}];
Vdd[0] = Interpolation[
  Join[{{{-L, -L, -L, intn[0][[1, 1, 1, 4]]}}}, 
   intn[0], {{{L, L, L, intn[0][[np, np, np, 4]]}}}]]
Do[sol[s] = 
  NDSolveValue[{-I D[[Psi][x, y, z, t], t] - 
       1/2 Laplacian[[Psi][x, y, z, t], {x, y, z}] + 
       1/2 ([Gamma]^2 x^2 + [Nu]^2 y^2 + [Lambda]^2 z^2) [Psi][x, 
         y, z, t] + 
       4 [Pi] a Nat Abs[[Psi][x, y, z, t]]^2 [Psi][x, y, z, t] + 
       3 add Nat Vdd[s - 1][x, y, z] [Psi][x, y, z, 
         t] + [Gamma]QF Nat^(3/2)
         Abs[[Psi][x, y, z, t]]^3 [Psi][x, y, z, t] == 0,
     [Psi][x, y, z, T[[s]]] == 
      sol[s - 1][x, y, z, T[[s]]], [Psi][L, y, z, t] == 
      0, [Psi][-L, y, z, t] == 0,
     [Psi][x, L, z, t] == 0, [Psi][x, -L, z, t] == 
      0, [Psi][x, y, L, t] == 0, [Psi][x, y, -L, t] == 
      0}, [Psi], {t, T[[s]], T[[s + 1]]}, {x, -L, L}, {y, -L, 
     L}, {z, -L, L}, 
    Method -> {"MethodOfLines", 
      "SpatialDiscretization" -> {"TensorProductGrid", 
        "MinPoints" -> 40, "MaxPoints" -> np, 
        "DifferenceOrder" -> "Pseudospectral"}}] // Quiet;
nkx[s] = 
  Table[Sum[
    xweights[[i]] Exp[
      I xpoints[[j]] xpoints[[i]]] Abs[
       sol[s][xpoints[[i]], 0, 0, T[[s + 1]]]]^2, {i, 
     Length[xg]}], {j, Length[xg]}];
 nky[s] = 
  Table[Sum[
    yweights[[i]] Exp[
      I ypoints[[j]] ypoints[[i]]] Abs[
       sol[s][0, ypoints[[i]], 0, T[[s + 1]]]]^2, {i, 
     Length[yg]}], {j, Length[yg]}];
 nkz[s] = 
  Table[Sum[
    zweights[[i]] Exp[
      I zpoints[[j]] zpoints[[i]]] Abs[
       sol[s][0, 0, zpoints[[i]], T[[s + 1]]]]^2, {i, 
     Length[zg]}], {j, Length[zg]}];
 finalnk[s] = nkx[s] nky[s] nkz[s];
intn[s] = 
  1/(6 [Pi]^2)
    angle Table[{xpoints[[j]], ypoints[[k]], zpoints[[m]], 
     Re[Sum[xweights[[j]] yweights[[k]] zweights[[
         m]] Exp[-I xpoints[[j]] xpoints[[i]]]  Exp[-I ypoints[[
           k]] ypoints[[i]]]  Exp[-I zpoints[[m]] zpoints[[i]]] ((
          3 zpoints[[m]]^2)/(
          xpoints[[j]]^2 + ypoints[[k]]^2 + zpoints[[m]]^2) - 
          1) finalnk[s][[i]], {i, Length[xg]}]]}, {j, Length[xg]}, {k,
      Length[yg]}, {m, Length[zg]}];
Vdd[s] = 
  Interpolation[
   Join[{{{-L, -L, -L, intn[s][[1, 1, 1, 4]]}}}, 
    intn[s], {{{L, L, L, intn[s][[np, np, np, 4]]}}}]];, {s, 1, 15}]
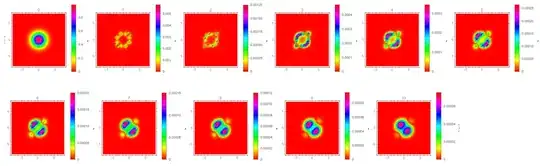
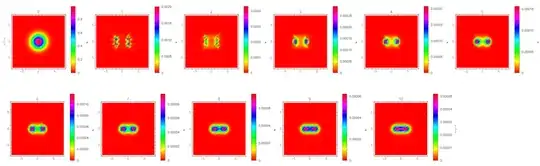
DensityPlot[
 Abs[sol[10][x, y, 0, T[[10 + 1]]]]^2, {x, -L, L}, {y, -L, L}, 
 ColorFunction -> "BlueGreenYellow", PlotPoints -> 200, Frame -> True,
  FrameTicks -> Automatic, LabelStyle -> {24, Bold, Large, Black}, 
 FrameLabel -> {{Style["y", FontFamily -> "Times New Roman", 
     FontSlant -> "Italic", FontWeight -> Bold, FontSize -> 30], 
    None}, {Style["x", FontFamily -> "Times New Roman", 
     FontSlant -> "Italic", FontWeight -> Bold, FontSize -> 30], 
    None}}]

The first error: you declare: intn[0] = 1/(6 [Pi]^2) but later you use: intn[0][[1, 1, 1, 4]] — Daniel Huber, Sep 20 '22 at 10:20
@AlexTrounev I posted the pictures from arxiv.org/pdf/2205.05193.pdf. Though this work https://arxiv.org/pdf/2202.13264.pdf also deals with the same equation. The formulation to avoid the singularity at the center is given in https://arxiv.org/pdf/1506.03283.pdf. Singularity arrives for large np in intn[0] in the code and I could not figure out the interpolation in vdd[0]. — Argha Debnath, Sep 24 '22 at 16:31
@ArghaDebnath It is not clear how they compute 3D states. As I remember we used Mathematica FEM in our report https://www.researchgate.net/publication/329642729_Formation_of_quantum_vortices_in_a_rotating_sphere_in_an_electromagnetic_field — Alex Trounev, Sep 25 '22 at 08:03
@AlexTrounev I will study the paper. I have one question regarding your previous solution https://mathematica.stackexchange.com/questions/209951/solving-partial-integro-differential-equation?rq=1. Why did you put f[m]'[t] instead of f[m][t]' as it is a time derivative d/dt in your "Now we can make a system of equations" section. — Argha Debnath, Sep 25 '22 at 08:17
@AlexTrounev In your paper https://www.researchgate.net/publication/329642729_Formation_of_quantum_vortices_in_a_rotating_sphere_in_an_electromagnetic_field your expression of A in Eq.(13) is very similar to mine and it also has a singularity at r=0. — Argha Debnath, Sep 25 '22 at 08:50
@AlexTrounev to avoid singularity I think this paper https://arxiv.org/pdf/0905.0386.pdf will be helpful. Check page 62 Eq.(A.3). — Argha Debnath, Sep 25 '22 at 09:04
@AlexTrounev I have another question regarding your previous program https://mathematica.stackexchange.com/questions/176171/ndsolve-aborted in electromagnetic case. Why you took gamma[t-x-y]; — Argha Debnath, Sep 25 '22 at 09:06
@ArghaDebnath This is plane wave $\exp{(i\omega t -i k_x x-i k_y y)}$. Regardless to f[m]'[t] I don't understand you question. Derivative is f[m]'[t] not f[m][t]' — Alex Trounev, Sep 25 '22 at 09:51
@AlexTrounev I am little bit confused as u(x,t)->f[m][t]. So if we take d/dt then f[m][t]' — Argha Debnath, Sep 25 '22 at 10:01
@ArghaDebnath No, f[m]=g is a symbol, g[t] is function, and g'[t] is derivative, — Alex Trounev, Sep 25 '22 at 15:13
@AlexTrounev Thanks for the explanations. Fortran program for 3D named imag3d can be found here http://cpc.cs.qub.ac.uk/summaries/AEWL_v1_0.html written by the same authors as https://arxiv.org/pdf/2202.13264.pdf. But it's in Fortran. — Argha Debnath, Sep 25 '22 at 16:42
@AlexTrounev The FORTRAN programs are in https://elsevier.digitalcommonsdata.com/datasets/5v7xsns8zm/1. — Argha Debnath, Sep 26 '22 at 13:07

score 2 · Accepted Answer · answered Sep 28 '22 at 04:18

3D case can be solved with a linear Mathematica FEM in imaginary time. But there are no stationary states for the chosen set of parameters. We need about 1 min to compute 1 step. First step looks like picture in the paper.

Needs["NDSolve`FEM`"];
Needs["NumericalDifferentialEquationAnalysis`"];
Lx = 8; Ly = 8; Lz = 8; np = 10; xg = 
 GaussianQuadratureWeights[np, -Lx, Lx]; xpoints = xg[[All, 1]];
xweights = xg[[All, 2]];
yg = GaussianQuadratureWeights[np, -Ly, Ly]; ypoints = yg[[All, 1]];
yweights = yg[[All, 2]];
zg = GaussianQuadratureWeights[np, -Lz, Lz]; zpoints = zg[[All, 1]];
zweights = zg[[All, 2]]; mesh = 
 ToElementMesh[Cuboid[{-Lx, -Ly, -Lz}, {Lx, Ly, Lz}], 
  MaxCellMeasure -> 0.25]
sol[0][x_, y_, z_] := E^(-(x^2 + y^2 + z^2)/4);
[Omega]x = 45; [Omega]y = 45; [Omega]z = 133; gmean[Omega] = (

[Omega]x [Omega]y [Omega]z)^(1/3); [Gamma] = [Omega]x/
  gmean[Omega]; [Lambda] = [Omega]z/
  gmean[Omega]; [Nu] = [Omega]y/gmean[Omega];
a0 = 5.29*10^-5; a = 85 a0; add = 131 a0; [Epsilon]dd = add/a;
[Gamma]QF = 
 128/3 Sqrt[[Pi] a^5] (1 + 
    1.5 [Epsilon]dd^2); angle = ((3 Cos[[Phi]]^2 - 1)/2); [Phi] = 0;
Nat = 10^6; nt = 10; dt = 1/10; c0 = angle 4 Pi/3/(2 Pi)^3;
nk[0] = Table[
   Sum[xweights[[i1]] yweights[[i2]] zweights[[i3]] Exp[
      I xpoints[[j1]] xpoints[[i1]] + I ypoints[[j2]] ypoints[[i2]] + 
       I zpoints[[j3]] zpoints[[i3]]] Abs[
       sol[0][xpoints[[i1]], ypoints[[i2]], zpoints[[i3]]]]^2, {i1, 
     Length[xg]}, {i2, Length[yg]}, {i3, Length[zg]}], {j1, 
    Length[xg]}, {j2, Length[yg]}, {j3, Length[zg]}];
int = Flatten[
   Table[{{xpoints[[j]], ypoints[[k]], zpoints[[m]]}, 
     c0 Re[Sum[
        xweights[[i1]] yweights[[i2]] zweights[[
          i3]] Exp[-I xpoints[[j]] xpoints[[i1]]] Exp[-I ypoints[[
            k]] ypoints[[i2]]] Exp[-I zpoints[[m]] zpoints[[
            i3]]] ((3 zpoints[[i3]]^2)/(xpoints[[i1]]^2 + 
              ypoints[[i2]]^2 + zpoints[[i3]]^2) - 1) nk[0][[i1, i2, 
          i3]], {i1, Length[xg]}, {i2, Length[yg]}, {i3, 
         Length[zg]}]]}, {j, Length[xg]}, {k, Length[yg]}, {m, 
     Length[zg]}], 2];
intn[0] = 
 Join[Flatten[Table[{{-Lx, y, z}, 0}, {y, ypoints}, {z, zpoints}], 1],
   Flatten[Table[{{x, -Ly, z}, 0}, {x, xpoints}, {z, zpoints}], 1], 
  Flatten[Table[{{x, y, -Lz}, 0}, {x, xpoints}, {y, ypoints}], 1], 
  int, Flatten[Table[{{Lx, y, z}, 0}, {y, ypoints}, {z, zpoints}], 1],
   Flatten[Table[{{x, Ly, z}, 0}, {x, xpoints}, {z, zpoints}], 1], 
  Flatten[Table[{{x, y, Lz}, 0}, {x, xpoints}, {y, ypoints}], 1]]; 
Vdd[0] = Interpolation[intn[0], InterpolationOrder -> 1];
Do[sol[s] = 
    NDSolveValue[{ ([Psi][x, y, z] - sol[s - 1][x, y, z])/dt - 
         1/2 Laplacian[[Psi][x, y, z], {x, y, z}] + 
         1/2 ([Gamma]^2 x^2 + [Nu]^2 y^2 + [Lambda]^2 z^2) [Psi][
           x, y, z] + 
         4 [Pi] a Nat Abs[sol[s - 1][x, y, z]]^2 [Psi][x, y, z] + 
         3 add Nat Vdd[s - 1][x, y, z] [Psi][x, y, 
           z] + [Gamma]QF Nat^(3/2) Abs[
            sol[s - 1][x, y, z]]^3 [Psi][x, y, z] == 0, 
       DirichletCondition[[Psi][x, y, z] == sol[0][x, y, z], 
        True]}, [Psi], Element[{x, y, z}, mesh]] // Quiet;
   nk[s] = 
    Table[Sum[
      xweights[[i1]] yweights[[i2]] zweights[[i3]] Exp[
        I xpoints[[j1]] xpoints[[i1]] + 
         I ypoints[[j2]] ypoints[[i2]] + 
         I zpoints[[j3]] zpoints[[i3]]] Abs[
         sol[s][xpoints[[i1]], ypoints[[i2]], zpoints[[i3]]]]^2, {i1, 
       Length[xg]}, {i2, Length[yg]}, {i3, Length[zg]}], {j1, 
      Length[xg]}, {j2, Length[yg]}, {j3, Length[zg]}];
   int = 
    Flatten[Table[{{xpoints[[j]], ypoints[[k]], zpoints[[m]]}, 
       c0 Re[Sum[
          xweights[[i1]] yweights[[i2]] zweights[[
            i3]] Exp[-I xpoints[[j]] xpoints[[i1]]] Exp[-I ypoints[[
              k]] ypoints[[i2]]] Exp[-I zpoints[[m]] zpoints[[
              i3]]] ((3 zpoints[[i3]]^2)/(xpoints[[i1]]^2 + 
                ypoints[[i2]]^2 + zpoints[[i3]]^2) - 1) nk[s][[i1, i2,
             i3]], {i1, Length[xg]}, {i2, Length[yg]}, {i3, 
           Length[zg]}]]}, {j, Length[xg]}, {k, Length[yg]}, {m, 
       Length[zg]}], 2];
   intn[s] = 
    Join[Flatten[Table[{{-Lx, y, z}, 0}, {y, ypoints}, {z, zpoints}], 
      1], Flatten[Table[{{x, -Ly, z}, 0}, {x, xpoints}, {z, zpoints}],
       1], Flatten[
      Table[{{x, y, -Lz}, 0}, {x, xpoints}, {y, ypoints}], 1], int, 
     Flatten[Table[{{Lx, y, z}, 0}, {y, ypoints}, {z, zpoints}], 1], 
     Flatten[Table[{{x, Ly, z}, 0}, {x, xpoints}, {z, zpoints}], 1], 
     Flatten[Table[{{x, y, Lz}, 0}, {x, xpoints}, {y, ypoints}], 1]]; 
   Vdd[s] = Interpolation[intn[s], InterpolationOrder -> 1];, {s, 1, nt}] // AbsoluteTiming

Visualization in cross-section $z=0$

Table[DensityPlot[Abs[sol[i][x, y, 0]], {x, -Lx, Lx}, {y, -Ly, Ly}, 
  ColorFunction -> Hue, PlotLegends -> Automatic, PlotLabel -> i, 
  PlotRange -> All, PlotPoints -> 50], {i, 0, nt}]

Visualization in cross-section $y=0$

Table[DensityPlot[Abs[sol[i][x, 0, z]], {x, -Lx, Lx}, {z, -Lz, Lz}, 
  ColorFunction -> Hue, PlotLegends -> Automatic, PlotLabel -> i, 
  PlotRange -> All, PlotPoints -> 50], {i, 0, nt}]

Thanks for your solution @AlexTrounev. I like how you used join in int[0] and discretized the time derivative. Indeed the first step looks like the figures in the paper but after some iterations, the segregated parts are again rejoined with two maxima. Any idea why? Which iteration step will be safe to say it is the final solution? If you can help me further with the energy terms: Ekin and Edip and the phase, it will be very helpful. — Argha Debnath, Sep 28 '22 at 07:20
@ArghaDebnath In the paper they did not discuss the numerical method used to compute results. We can try to reproduce what they did, but it takes time. — Alex Trounev, Oct 03 '22 at 05:23
It's alright @AlexTrounev. Thanks again for what you have done. — Argha Debnath, Oct 03 '22 at 05:42

Solving 3D Nonlinear Integral Partial Differential Equation

1 Answers1