I have an action given by, $$S = \int dx \frac{1}{z^d} \sqrt{-f(z,u) u'^2 - 2 u' z' +1}$$
The dependent variables are $u$ and $z$ for which they are dependent on the parameter $x$. The equation of motion (EOM) can be calculated by,
$$\frac{\partial L}{\partial z'} = \frac{-u'}{z^d \sqrt{-f u'^2 - 2 u' z' +1}}\\ \frac{\partial L}{\partial z} = \frac{-u'^2 \partial_z f}{2 z^d \sqrt{-f u'^2 - 2 u' z' +1}}\\ \frac{\partial L}{\partial u'} = \frac{-f u' -z'}{z^d \sqrt{-f u'^2 - 2 u' z' +1}}\\ \frac{\partial L}{\partial u} = \frac{-u'^2 \partial_u f}{2 z^d \sqrt{-f u'^2 - 2 u' z' +1}}$$
where (I have written $f$ only to declutter)
$$f(z,u) = 1 - m(u) z^{d+1}, \qquad \frac{d}{dx} f = \left( \partial_z f \right) z' + \left( \partial_u f \right) u'$$
EOM for $z$: $\frac{d}{dx}\frac{\partial L}{\partial z'} - \frac{\partial L}{\partial z} = 0$
EOM for $u$: $\frac{d}{dx}\frac{\partial L}{\partial u'} - \frac{\partial L}{\partial u} = 0$
The boundary conditions (BC) are,
$z(x_0) = \epsilon, z'(x_s) = 0, u(x_0) = t, u'(x_s) = 0$
where the domain is $[x_0, x_s]$, $\epsilon$ is some arbitrary small number, and $t$ represents time for which I can choose some value.
I have not shown all the details, just the general picture of what I'm using. The details are in the code below.
d = 4;
x0 = 10^-5;
xs = 1;
c = 10^-2;
m0 = 1;
m[x_] := ((d + 1)/(c u[x] + (d + 1) m0^(-1/(d + 1))))^(d + 1);
f[x_] := 1 - m[x] z[x]^(d + 1);
fu[x_] := c z[x]^(d + 1) m[x]^((d + 2)/(d + 1));(*partial u*)
fz[x_] := -(d + 1) m[x] z[x]^d;(*partial z*)
fp[x_] := fz[x] z'[x] + fu[x] u'[x];(*x derivative of f*)
EOMz = -2 z[x]^d u''[x] - 2 z[x]^d u'[x]^2 z''[x] + (2 d f[x]^2 z[x]^(d - 1) - f[x] fz[x] z[x]^d) u'[x]^4 + (6 d f[x] z[x]^(d - 1) - 2 fz[x] z[x]^d) u'[x]^3 z'[x] + 4 d z[x]^(d - 1) u'[x]^2 z'[x]^2 - fp[x] z[x]^d u'[x]^3 + (fz[x] z[x]^d - 4 d f[x] z[x]^(d - 1)) u'[x]^2 - 6 d z[x]^(d - 1) u'[x] z'[x] + 2 d z[x]^(d - 1);
EOMu = -2 f[x] z[x]^d u''[x] + (2 z[x]^d u'[x] z'[x] - 2 z[x]^d) z''[x] - 2 d f[x]^2 z[x]^(d - 1) u'[x]^3 z'[x] - 4 d z[x]^(d - 1) u'[x] z'[x]^3 - 6 d f[x] z[x]^(d - 1) u'[x]^2 z'[x]^2 + fp[x] z[x]^d u'[x]^2 z'[x] + 2 d f[x] z[x]^(d - 1) u'[x] z'[x] + 2 d z[x]^(d - 1) z'[x]^2 - fp[x] z[x]^d u'[x];
s = NDSolveValue[Rationalize[{EOMz == 0, EOMu == 0, z[x0] == 10^-5, z'[xs] == 10^-16, u[x0] == 1, u'[xs] == 10^-16}, 0], {z, u}, {x, x0, xs}, Method -> {"Shooting", "StartingInitialConditions" -> {z[x0] == 10^-5, z'[x0] == 10^6, u[x0] == 1, u'[x0] == 10^-3}}, WorkingPrecision -> 20]
NDSolveValue::ndsz: At x == 0.99999810922483170542600892434185908076`20., step size is effectively zero; singularity or stiff system suspected.
Some comments about the code: I have chosen $10^{-16}$ for the vanishing derivatives at $x_s$ which is effectively zero, I chose $t = 1$. I employed shooting method for which I know that $z(x)$ should rapidly have a large value at the start so I guessed $z'(x_0) = 10^6$, for $u(x)$ I'm not sure of its initial behavior so I just guessed $u'(x_0) = 10^{-3}$. I have arbitrarily chosen some values for the initial mass $m_0$, the constant $c$, and the domain $[x_0, x_s]$.
The equations I have are coupled nonlinear second-order differential equations. As you see, Mathematica complains that the system of equations is stiff, I guess this can be alleviated by rescaling. However, I can first try to change the values of $m_0$ and $c$ to see if that will bring any changes, alas, none of it is working. Any advice on how to tackle this kind of problem?
*I don't suppose that Numerical GR techniques are needed in this case, however, I may be wrong.
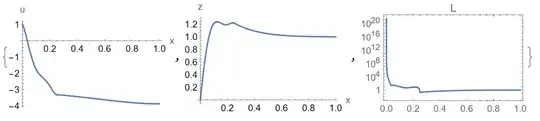
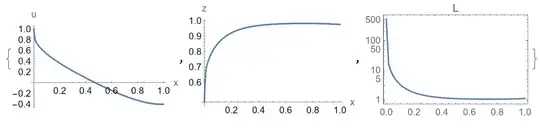
Sreal or complex? IfLis real, then we have additional constraint $-f(z,u) u'^2 - 2 u' z' +1\ge 0$ – Alex Trounev Nov 03 '22 at 11:45ShootingwithMethod -> {"StiffnessSwitching", "NonstiffTest" -> False}, the stiffness issue is gone but it is replaced by an issue about Complex Infinity which I guess is what you're talking about. However, I'm not sure where is that coming from. – mathemania Nov 03 '22 at 12:46