NDSolve unable to solve nonlinear differential equation

Question

I have an action $S$,

$$S = \int dx \frac{1}{z^d} \sqrt{1 + \frac{z'(x)^2}{f(z)}}$$

where the Lagrangian $L$ is,

$$L = \frac{1}{z^d} \sqrt{1 + \frac{z'(x)^2}{f(z)}}$$

I want to plot $z(x)$ and solve the value of $S$, however, I encountered some error. The equations of motion (EOM) are nonlinear and I know they can be solved using some numerical approximation techniques, actually, this post is related to (275496) where @AlexTrounev used the wavelet approach. The Lagrangian there is much more complicated than what is here, however, I found that they produced similar errors using NDSolve.

Actually, the Lagrangian here has a conserved quantity which allowed me to simplify $S$ by hand and solve it with the help of Mathematica. The reason I'm posting this is that I'm hoping that NDSolve can fully solve the EOM without resorting to conservation quantities since the Lagrangian is much simpler but that didn't work. I want to know if it is an NDSolve issue where it cannot find the correct technique (thus needing the wavelet approach) or an equation issue.

I want to emphasize that I really want to know what part of the equation is causing the issue (which was not cleared in the other post) so that I can understand it better.

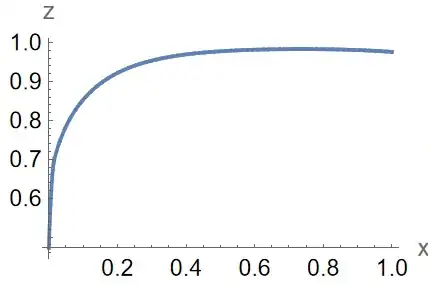
The plot of $z(x)$ should have the form shown in a sample below (disregarding the scale/values on the axes),

Needs["VariationalMethods`"]
f = 1 - (z[x]/zh)^(d + 1);
L = Sqrt[1 + (z'[x]^2/f)]/z[x]^d;
eqeuler = EulerEquations[L, z[x], x];
wp = 20;
equations = SetPrecision[{eqeuler /. {d -> 3, zh -> 10}, z[10^-5] == 10^-5, z'[10] == 0}, wp];
eq = equations[[1]];
bc1 = equations[[2]];
bc2 = equations[[3]];
sols = NDSolve[{eq, bc1, bc2}, z, {x, 10^-5, 10}, Method -> "StiffnessSwitching", WorkingPrecision -> wp]
Power::infy: Infinite expression 1/0^3 encountered.
Power::infy: Infinite expression 1/0^4 encountered.
Infinity::indet: Indeterminate expression 0 ComplexInfinity encountered.
Power::infy: Infinite expression 1/0^3 encountered.
General::stop: Further output of Power::infy will be suppressed during this calculation.
Infinity::indet: Indeterminate expression 0 ComplexInfinity encountered.
Infinity::indet: Indeterminate expression 0 ComplexInfinity ComplexInfinity encountered.
General::stop: Further output of Infinity::indet will be suppressed during this calculation.
NDSolve::ndnum: Encountered non-numerical value for a derivative at x == 1.`20.*^-5.
Plot[Evaluate[z[x] /. sols], {x, 10^-5, 10}, AspectRatio -> 3/4, Frame -> True, FrameLabel -> {"x", "z"}, PlotStyle -> {Blue, 24}, LabelStyle -> {Black, 20}, PlotRange -> Full, ImageSize -> Large, AspectRatio -> 3/4]

Update I have tried the shooting method as advised in the posts (237117) (72725), however, I still encounter problems like step size is effectively zero; singularity or stiff system suspected. I'm not sure if shooting method is the best way.

Answer 1

We can solve this problem with "ExplicitEuler" as follows. First, we define equations

Needs["VariationalMethods`"];
f = 1 - (z[x]/zh)^(d + 1);
L = Sqrt[1 + (z'[x]^2/f)]/z[x]^d;
eqeuler = EulerEquations[L, z[x], x];
eq = eqeuler /. {d -> 3, zh -> 10}; bc = {z[10^-5] == 10^-5, 
  v[10] == 0};
s = Solve[eq, z''[x]][[1]] // Simplify;
eq01 = {v'[x] == s[[1, 2]] /. z'[x] -> v[x], z'[x] == v[x]};

Second, we define function

zm[e_?NumericQ] := 
 Module[{eps = e, s1}, 
  s1 = NDSolveValue[{eq01, z[10] == eps, v[10] == 0}, 
    z[10^-5], {x, 10^-5, 10}, Method -> "ExplicitEuler", 
    StartingStepSize -> 10^-4]; s1];

Third, we compute root

sol = 
 FindRoot[zm[e] == 10^-5, {e, 991/100}, WorkingPrecision -> 30] // 
  Quiet
(Out[]= {e -> 9.90980851516520491227795116651})

Check that sol gives initial condition with error of 10^-10

zm[e] /. sol
Out[]= 0.0000100001

Finally, we compute and plot solution

Z = NDSolveValue[{eq01, z[10] == e /. sol, v[10] == 0}, 
  z, {x, 10^-5, 10}, Method -> "ExplicitEuler", 
  StartingStepSize -> 10^-4];
Plot[Z[x], {x, 10^-5, 10}, Frame -> True, PlotRange -> All]