Numerical solution of a partial derivative problem

Question

WARNING: a couple of days ago I posted a similar question, but due to the impossibility of DirichletCondition[] to handle "cross-coupling of dependent variables" I thought of reformulating the same problem using a single function.

The goal is to find a function $f : \Omega \subset \mathbb{R}^2 \to \mathbb{R}$ such that:

$$ \begin{cases} \Delta f = 0 & \text{on} \; \Omega \\ \frac{\text{d}}{\text{d} n} f = y\,n_x - x\,n_y & \text{on} \; \partial\Omega \end{cases} $$

with $n = (n_x,\,n_y)$ exterior normal vector to $\partial\Omega$.

Therefore, once the following plane region is defined:

c[x_, y_] := 2 x^2 + 3 y^2
{nx, ny} = Grad[c[x, y], {x, y}];
Ω = ImplicitRegion[c[x, y] <= 1, {x, y}];
RegionPlot[Ω, AspectRatio -> Automatic]

I tried to set the problem by writing:

bcs = NeumannValue[y nx - x ny, True];
fsol = NDSolveValue[Laplacian[f[x, y], {x, y}] == bcs, f, {x, y} ∈ Ω];
Plot3D[fsol[x, y], {x, y} ∈ Ω]

but unfortunately I got tons of warnings:

NDSolveValue::femibcnd: No DirichletCondition or Robin-type NeumannValue was specified for {f}; the result may not be unique.

LinearSolve::parpiv: Zero pivot was detected during the numerical factorization or there was a problem in the iterative refinement process. It is possible that the matrix is ill-conditioned or singular.

NDSolveValue::fempsf: PDESolve could not find a solution.

and I just can't figure out what I'm doing wrong. Ideas? Thank you!

EDIT 1: copying the code of user21 I wrote the following routine:

Needs["NDSolve`FEM`"];
DiniNeumann[f_, Ω_] := Module[
  {dpde, dbc, vd, sd, mdata, g, load, stiffness, damping, mass, 
   prec, dof, loadContribution, stiffnessContribution, initCoeffs, 
   constraintMatrix, constraintRows, constraintValueMatrix},
  {dpde, dbc, vd, sd, mdata} = Quiet[ProcessPDEEquations[
     {Laplacian[g[x, y], {x, y}] == NeumannValue[f, True]}, g, 
     {x, y} ∈ Ω]]; {load, stiffness, damping, mass} = dpde["All"];
  DeployBoundaryConditions[{load, stiffness}, dbc];
  prec = mdata["Precision"]; dof = mdata["DegreesOfFreedom"];
  loadContribution = SparseArray[{}, {dof, 1}, N[0, prec]];
  stiffnessContribution = SparseArray[{}, {dof, dof}, N[0, prec]];
  initCoeffs = InitializePDECoefficients[vd, sd, 
    "LoadCoefficients" -> {{1}}]; 
  constraintMatrix = Transpose[DiscretizePDE[initCoeffs, mdata, 
    sd]["LoadVector"]]; constraintRows = {1}; 
  constraintValueMatrix = SparseArray[{{N[0, prec]}}];
  dbc = DiscretizedBoundaryConditionData[{loadContribution, 
    stiffnessContribution, constraintMatrix, constraintRows, 
    constraintValueMatrix, {dof, 0, Length[constraintRows]}}, 1];
  DeployBoundaryConditions[{load, stiffness}, dbc, 
   "ConstraintMethod" -> "Append"]; ElementMeshInterpolation[{Ω}, 
   Take[LinearSolve[stiffness, load], mdata["DegreesOfFreedom"]]]]

thanks to which it's sufficient to write:

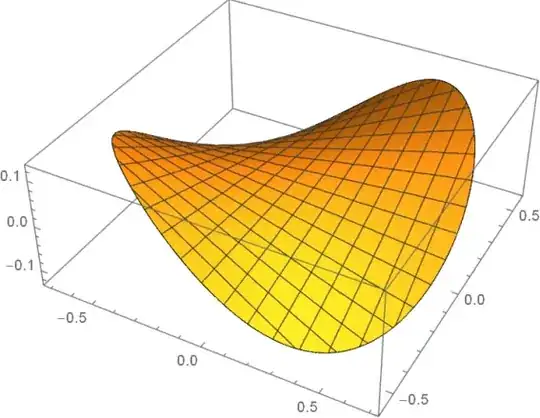
Ω = ToElementMesh@ImplicitRegion[2 x^2 + 3 y^2 <= 1, {x, y}];
f = DiniNeumann[y (4 x) - x (6 y), Ω];
Plot3D[f[x, y], {x, y} ∈ Ω]

to get what you want:

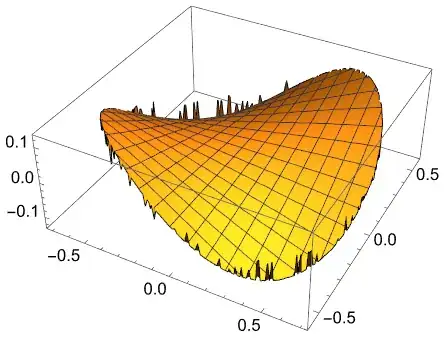
EDIT 2: thanks to suggestions from Ulrich Neumann and user21, writing:

Needs["NDSolve`FEM`"];
Ω = ToElementMesh[ImplicitRegion[2 x^2 + 3 y^2 <= 1, {x, y}], 
                  "IncludePoints" -> {{0, 0}}];
fsol = NDSolveValue[{Laplacian[f[x, y], {x, y}] == NeumannValue[y (4 x) - x (6 y), 
                     True], DirichletCondition[f[x, y] == 0, x == 0 && y == 0]}, 
                     f, {x, y} ∈ Ω];
Plot3D[fsol[x, y], {x, y} ∈ Ω]

I get:

which apparently is lower quality than what you got above (at least using the version 13.1.0 for Microsoft Windows (64-bit) (August 14, 2022)).

EDIT 3: in version 13.2.0 for Microsoft Windows (64-bit) (November 18, 2022) the plot is smooth, all fixed!

Pure Neumann b.c. is a bit troublesome: https://mathematica.stackexchange.com/q/191476/1871 — xzczd, Dec 03 '22 at 01:27
You don't need partial derivatives. The @user21`s solution(thanks for adding) and my solution are the same(up to a constant) — Ulrich Neumann, Dec 03 '22 at 13:44
@TeM If your larger problem is still a pure NeumannProblem, adding a DirichletCondition should work too! — Ulrich Neumann, Dec 03 '22 at 13:54

score 7 · Accepted Answer · answered Dec 03 '22 at 13:24

Solution of this Laplaceproblem is unique except for a constant. That's why it's necessary to add a Dirichletcondition(Don't know why it isn't sufficient to add bc of an inner point f[0,0]==0):

c[x_, y_] := 2 x^2 + 3 y^2
{nx, ny} = Grad[c[x, y], {x, y}];
[CapitalOmega] = ImplicitRegion[c[x, y] <= 1, {x, y}];

For Dirichletcondition we need to know one boundary point

xyRand = MeshCoordinates[BoundaryDiscretizeRegion[\[CapitalOmega]]];(* some boundary points*)
bcs = NeumannValue[y nx - x ny, True] 
fsol = NDSolveValue[{Laplacian[f[x, y], {x, y}] == NeumannValue[ -2 x y, True] , 
DirichletCondition[f[x, y] == 0,x == xyRand[[1, 1]] && y == xyRand[[1, 2]]]}, 
f, {x, y} [Element] [CapitalOmega] ] 
Plot3D[fsol[x, y], {x, y} [Element] [CapitalOmega]]

Comments are not for extended discussion; this conversation has been moved to chat. — Kuba, Dec 08 '22 at 09:44

Numerical solution of a partial derivative problem

1 Answers1

Linked