This post contains several code blocks, you can copy them easily with the help of importCode.
It's well known that, though DSolve is improved these years, it's still not strong enough, so let me add a solution based on finiteFourierCosTransform.
We first change the variable to make the b.c.s in x direction homogeneous:
Clear[b, h, g]
With[{f = f[x, y]}, {eq, bc} =
{Laplacian[f, {x, y}] == 0,
{D[f, x] == y /. x -> -b/2, D[f, x] == y /. x -> b/2,
D[f, y] == -x /. y -> -h/2, D[f, y] == -x /. y -> h/2}}];
solparti = Function[{x, y}, aa x^2 + bb y^2 + cc x y]
(* Function[{x, y}, aa x^2 + bb y^2 + cc x y] *)
{eq, bc[[;; 2]]} /. f -> solparti // Simplify // Flatten // DeleteDuplicates
rule = Solve[%, {aa, bb, cc}][[1]]
(* {aa + bb == 0, aa b + y == cc y, aa b + cc y == y} )
( {aa -> 0, bb -> 0, cc -> 1} *)
rulef = f -> ({x, y} |-> Evaluate[g[x, y] + solparti[x, y] /. rule])
(* f -> Function[{x, y}, x y + g[x, y]] *)
{neweq, newbc} = {eq, bc} /. rulef // Simplify
(* {Derivative[0, 2][g][x, y] + Derivative[2, 0][g][x, y] ==
0, {Derivative[1, 0][g][-(b/2), y] == 0, Derivative[1, 0][g][b/2, y] == 0,
2 x + Derivative[0, 1][g][x, -(h/2)] == 0, 2 x + Derivative[0, 1][g][x, h/2] == 0}} *)
Then we make the transform. (Definition of finiteFourierCosTransform isn't included in this post, please find it in the link above. )
Format@finiteFourierCosTransform[a_, __] := ℱ[a]
Assuming[{b > 0},
finiteFourierCosTransform[{neweq, newbc[[3 ;;]]}, {x, -b/2, b/2}, n] /.
Rule @@@ newbc[[;; 2]]]
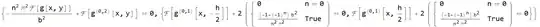
tsys = % /. a_finiteFourierCosTransform :> a[[1]]
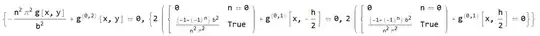
tsol0 = DSolveValue[Simplify[tsys, n == 0], g[x, y], y]
tsol = DSolveValue[Simplify[tsys, n > 0], g[x, y], y]
tsolgeneral = Piecewise[{{tsol, n > 0}}, tsol0]
sol = inverseFiniteFourierCosTransform[tsolgeneral, n, {x, -b/2, b/2}] /.
C[1] -> [ScriptCapitalC]
solfinal = f[x, y] /. rulef /. g[x, y] -> sol /. C -> Infinity

When calculating tsol0, there's a DSolveValue::bvsing warning. This is expected, because we haven't used the constraint at $(0,0)$. Symbolically calculating \[ScriptCapitalC] is too expensive (Frankly speaking, I'm not sure if Sum is capable of calculating it. ) So let's simply keep in mind that the \[ScriptCapitalC] is a constant that makes the solution be 0 at $(0,0)$.
Check with first 50 terms of the series:
tst = solfinal /. Infinity -> 50 /. \[ScriptCapitalC] -> 0 // ReleaseHold;
Seems that \[ScriptCapitalC] == 0:
tst /. {x -> 0, y -> 0}
(* 0 *)
Block[{b = 100, h = 200},
Plot3D[tst, {x, -b/2, b/2}, {y, -h/2, h/2}, AxesLabel -> Automatic]]

Remark
Actually it's not necessary to make the b.c.s homogeneous. Then we'll obtain the following solution:
Assuming[{b > 0},
finiteFourierCosTransform[{eq, bc[[3 ;;]]}, {x, -b/2, b/2}, n] /.
Rule @@@ bc[[;; 2]]];
tsys = % /. a_finiteFourierCosTransform :> a[[1]];
tsol0 = DSolveValue[Simplify[tsys, n == 0], f[x, y], y];
tsol = DSolveValue[Simplify[tsys, n > 0], f[x, y], y];
tsolgeneral = Piecewise[{{tsol, n > 0}}, tsol0];
sol = inverseFiniteFourierCosTransform[tsolgeneral, n, {x, -b/2, b/2}] /.
C[1] -> [ScriptCapitalC] /. C -> Infinity

This solution is definitely correct, but a bit confusing, because you'll find the b.c. in x direction isn't satisfied!:
tst2 = sol /. Infinity -> 50 /. \[ScriptCapitalC] -> 0 // ReleaseHold;
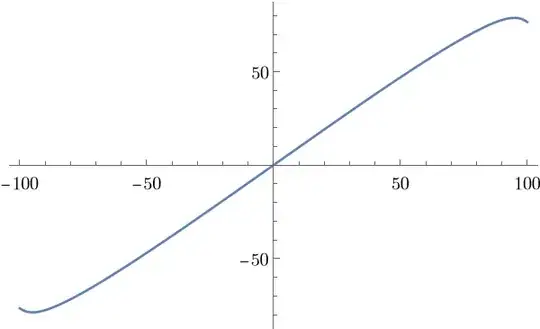
Block[{b = 100, h = 200}, Plot[D[tst2, x] /. x -> b/2 // Evaluate, {y, -h/2, h/2}]]

Why? This is all because of the property of Fourier cosine series. If we stagger the boundary a bit, we'll see a reasonable output:
Block[{b = 100, h = 200, approx = 0.9},
Plot[D[tst2, x] /. x -> -b/2 approx // Evaluate, {y, -h/2, h/2}]]

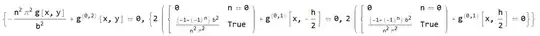






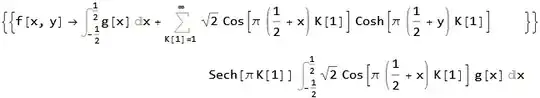
DSolveis incorrect, it should beLaplacian[f[x, y], {x, y}] == 0, {Derivative[1, 0][f][-b/2, y] == y, Derivative[1, 0][f][+b/2, y] == y, Derivative[0, 1][f][x, -h/2] == -x, Derivative[0, 1][f][x, +h/2] == -x}. Correcting this doesn't resolve the issue, of course. – xzczd Feb 20 '23 at 15:13