8

I have a messy expression of variables that I would like to simplify under the assumption that certain ratios of the variables are small. For example, consider $\sqrt{x+y}\;$ expanded for small $\frac{y}{x}$. That is, $x >> y$. This is simple enough to do by hand (pull out a $\sqrt{x}$ and then define a new variable to be $\frac{y}{x}$, then expand this variable about $0$). But, I cannot figure out how to do it in Mathematica.

EDIT 1

I've since realized that what I actually want to do is more complicated than the example above. Consider the following expression $\sqrt{a+d} + \sqrt{b+d}\;$ expanded for small $\frac{d}{a}$ and small $\frac{d}{b}$ (that is $a>>d$ and $b>>d$). Following Artes' answer below, the solution is 

Series[ (a + d)^(1/2) + (b + d)^(1/2) /. {d -> z1 a, d -> z2}, {z1, 0, 2},{z2, 0, 2}] /. 
{z1 -> d/a, z2 -> d/b}

But this solution doesn't work as intended due to the order operations Mathematica performs upon this command. What needs to be done is to replace d with z1 a, then expand z1 about 0, replace z1 with d/a, then replace d with z2 b, expand z2 about 0, and finally replace z2 with d/b. How can one do this in Mathematica?
(Obviously the example I gave can be separated into two expressions when can be expanded separately, but this cannot be done for the more complicated expression I am actually trying to expand).

Artes
  • 57,212
  • 12
  • 157
  • 245
mcFreid
  • 183
  • 6
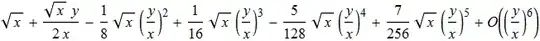
  • If this example can be simply worked out as you've observed then it won't be an appropriate one to present the issue. Try to provide another example which might be better suited for your real problem. You shouldn't use 0.5 since it means (in Mathematica) a machine precission number unlike 1/2 denoting an exact value. – Artes Jun 27 '13 at 17:30
  • From a mathematical point of view, this is a possible duplicate of Multivariable Taylor expansion does not work as expected. There are some practical differences, but I think they are very minor. – Jens Jun 28 '13 at 00:47

1 Answers1

8

There are options in Series (Analytic, Assumptions) which you might exploit. Nonetheless let's use a bit more straightforward approach, simply change the variable y (y -> z x) and then back z -> y/x:

Series[(x + y)^(1/2) /. y -> z x, {z, 0, 5}] /. z -> y/x // Quiet // TraditionalForm

enter image description here

Edit

Since the question has been edited we should add a few remarks.
In order to transform appropriately the Series results (its head is SeriesData) we should get rid of it with Normal (then we loose terms with powers (y/x)), e.g. 

Normal @ Series[(x + y)^(1/2) /. y -> z x, {z, 0, 5}] /. z -> y/x // TraditionalForm

enter image description here

Nonetheless we can transform appropriately expressions of the form (a + d)^(1/2) + (b + d)^(1/2) working with SeriesData if we define a simple function, e.g.

f[x_, y_, k_] := Series[(x + y)^k /. y -> z x, {z, 0, 5}] /. z -> y/x

(a + d)^(1/2) + (b + d)^(1/2) /. (x_ + y_)^k_ -> f[x, y, k] // Quiet // TraditionalForm

enter image description here

Alternatively we can expand a given expression around infinity, e.g.

Series[(a + d)^(1/2) + (b + d)^(1/2) /. {a -> v d, b -> w d},
       {v, Infinity, 5}, {w, Infinity, 5}] /.
{v -> a/ d, w -> b/d} // Quiet // TraditionalForm
Artes
  • 57,212
  • 12
  • 157
  • 245
  • much simpler than what I use, +1. – rcollyer Jun 27 '13 at 15:03
  • Ah, this makes sense. What if I have many ratio's I want to expand about? My expression is a function of a,b,c,d,e,f and I want to write it as an expansion for d,e,f << a,b,c. Is it valid to use ReplaceAll in steps? That is, first replace d with d/a, expand, then replace d with d/b, expand, etc... for each d,e,f. I could do this with a loop, obviously, but each Series expansion is already slow enough. Is there a way to do it using a similar method as your answer above? – mcFreid Jun 27 '13 at 15:14
  • @rcollyer Thanks for an upvote. – Artes Jun 27 '13 at 15:18
  • @mcFreid You could use just once ReplaceAll e.g. Series[...]/.{z1->d/a,z2->e/b,z3->f/c} and then change variables back. There are in 99% cases better ways than loops in Mathematica. – Artes Jun 27 '13 at 15:22
  • So there's no issue with Series[expr /. {d -> z1 a, d -> z2 b, d -> z3 c, e -> z4 a, e -> z5 b, e -> z6 c, f -> z7 a, f -> z8 b, f -> z9 c}] /. {z1 -> d/a, z2 -> d/b, etc...} ? – mcFreid Jun 27 '13 at 15:27
  • @mcFreid Keep in mind that you should appropriately include in Series where an expression expr should be expanded, what variables to use and how many terms you need, e.g. Series[expr /. listOfRules, {{z1, 0, 5}, {z2, 0, 3}, {z3, 0, 5}}]/.listOfReciprocalRules // Quiet. – Artes Jun 27 '13 at 15:35
  • Yup - just didn't put that in the question above. Sorry for the confusion. How does Mathematica handle the command? Ideally it would try (d -> z1 a), expand z1 about 0, apply (z1 -> d/a), then try (d -> z2 b) and go on. From the ordering of the code though, my feeling is that this would not be the case and instead it would never get to (d -> z2 b) because after (d -> z1 a) there are no d's left. – mcFreid Jun 27 '13 at 15:40
  • @mcFreid If you are not sure you've got a correct answer you should better wait a bit and then choose the best one to accept it. My experience is that one needs a certain well defined expression to work with and to provide the best possible solution. You can edit you question providing your (appropriately small) expression which might be a good example for any possible issues. Then I (or someone else) could add an answer which completely clarifies your problem. – Artes Jun 27 '13 at 15:53
  • I clarified my questions as requested. – mcFreid Jun 27 '13 at 17:09
  • @mcFreid So what, does the answer satisfy your needs now? – Artes Jan 05 '14 at 23:54