3

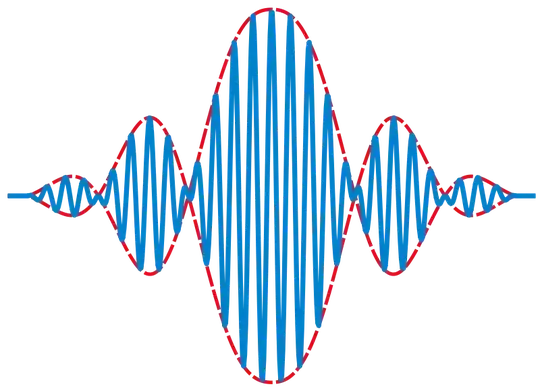
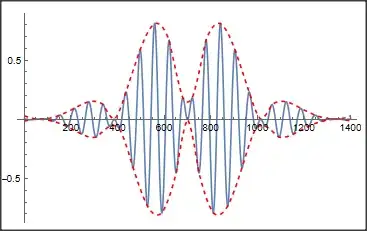
I have this wavepacket, which is defined over an interval $[a,b], \ a,b\in \mathbb{R}$. Suppose the wavepacket is complex trigonometric and analytic, then how can I find, using any formula or transform, the envelope function which is shown in red on the image below?

enter image description here

That envelope function would be actually two functions, as you can see the red dotted line is defined by two continuous functions $x_1(t)$ and $x_2(t)$ which is a continuous extension of the disjoint countable sets of suprema of the range of the wavefunction.

How are these two functions found? Thanks

Vangsnes
  • 591
  • 2
  • 9
  • 2
    may be these can help ? envelope-for-harmonic-oscillator and plotting-a-trig-functions-along-with-its-envelope I assumed you are asking how to draw the envelope. But I am not sure if are asking something else. – Nasser Jan 19 '23 at 08:43
  • @Nasser it may be that your Hilbert transform formula we discussed yesterday may be used to find the envelope function. However, can an envelope function be also a series with your Hilbert Transform formula? – Vangsnes Jan 19 '23 at 10:12
  • 1
    I think this is a difficult task. The maxima may not be the envelope points although they will approximate the envelope. It is sometimes argued that the envelope is in the viewers imagination... Your thoughts on Hilbert transforms are along the correct direction but that does not always work see here. – Hugh Jan 19 '23 at 14:50
  • @Hugh in those cases you refer to, the Hilbert transform didn't work because the norms of those function explodes towards infinity. One has to in that case generate a series over an interval to rectify that problem – Vangsnes Jan 19 '23 at 15:02

2 Answers2

5

We first need some data:

d = Table[Exp[-t^2/10] Sin[10 t] Sin[t], {t, -7, 7, 0.01}]; ListLinePlot[d, PlotRange -> All]

![enter image description here

Then we need a function that determines the local min/max:

mima[d_] := Module[{},
   Reap[
    Do[
     If[d[[i]] > d[[i + 1]] < d[[i + 2]], Sow[i + 1, 1]];
     If[d[[i]] < d[[i + 1]] > d[[i + 2]], Sow[i + 1, 2]];
     , {i, Length[d] - 2}]
    ]][[2]]

Now we can get the max/min and fit an interpolating function.

{mi, ma} = mima[d];
mi = Transpose[{Range[Length[d]], d}][[mi]]; fmi = Interpolation[mi];
ma = Transpose[{Range[Length[d]], d}][[ma]]; fma = Interpolation[ma];

Finally we draw everything:

Show[
 {ListLinePlot[d, PlotRange -> All], 
  Plot[{fmi[x], fma[x]}, {x, 0, Length[d]}, 
    PlotStyle -> {{Red, Dashed}, {Red, Dashed}}] // Quiet}]

enter image description here

Daniel Huber
  • 51,463
  • 1
  • 23
  • 57
  • Thanks Daniel, but are you able to extract the envelope function too from this calculation? Since I would like to find its derivatives. – Vangsnes Jan 19 '23 at 10:10
  • 1
    @Vangsnes, the fmi[x] and fma[x] in Daniel's answer are interpolation function objects that can be differentiated. However, you can't obtain the analytical form of the envelop function by this way of course. – Rom38 Jan 19 '23 at 10:13
  • 1
    @Vangsnes As Rom38 pointed out, fmi, fma are functions. If you want to fit an analytical expression, you can take the points in mi/ma. – Daniel Huber Jan 19 '23 at 10:23
  • So I can extract the points and do nonlinear regression ! – Vangsnes Jan 19 '23 at 13:43
  • 1
    @Vangsnes Yes. Non necessarily nonlinear, maybe a linear regression will do. The point are already contained in mi or ma. – Daniel Huber Jan 19 '23 at 15:01
  • Thanks Daniel, this I will keep for further use. – Vangsnes Jan 19 '23 at 15:03
3

The envelope can be detected using EstimatedBackGround after v10. A demo is available here.

Let's say the signal is defined as:

m[x_] := Cos[9 x] Sinc[x]; 
Plot[m[x], {x, -3 π, 3 π}, PlotRange -> All]

enter image description here

Sample the data and plot envelopes:

data2 = Table[m[x], {x, -10, 10, 0.05}];

ListLinePlot[{data2
  , EstimatedBackground[data2]
  , -EstimatedBackground[-data2]}
 , AspectRatio -> 2/3
 , ImageSize -> Medium
 , PlotRange -> {-1.2, 1.2}
 , PlotStyle -> {Thin, {Dashed, Red}
   , {Dashed, Red}
   }
 , Filling -> {2 -> {3}}
 , FillingStyle ->
  Lighter@Lighter@Yellow
 ]

enter image description here

Syed
  • 52,495
  • 4
  • 30
  • 85