Some ways of doing it:
With
x = {1, 2, 3};
y = {4, 5, 6};
all of the following
Thread[{x, y}] // MatrixForm
Transpose[{x, y}] // MatrixForm
Inner[List, x, y, List] // MatrixForm
MapThread[List, {x, y}] // MatrixForm
Table[{x[[i]], y[[i]]}, {i, 1, Length[x]}] // MatrixForm
Partition[Riffle[x, y], 2] // MatrixForm
Transpose[ArrayFlatten[{x, y}], {2, 1}] // MatrixForm
Function[, {##}, Listable][x, y] // MatrixForm
Quiet@Factor[x, y] /. Factor -> List // MatrixForm
a variant of the last is:
foo[x, y] /. foo -> List // MatrixForm
Edit 1: there'a a new command called ArrayReduce
ArrayReduce[Dot, {x, y}, 1] // MatrixForm
Edit 2: and another way
Multicolumn[Flatten@ArrayReshape[{x, y}, {2, 3}],
2][[1]] // MatrixForm
Edit 3: special thanks to @user1066 for the valuable comment. One can observe how the following behaves
ArrayReduce[f, {x, y}, 1] // MatrixForm
and from the above we can deduce that the following two commands give the desired output
ArrayReduce[Join, {x, y}, 1] // MatrixForm
ArrayReduce[Union, {x, y}, 1] // MatrixForm
All of the above give:


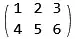


x = {1, 2, 3}; y = {4, 5, 6}; m2 = Transpose[{x, y}]– cvgmt Jan 30 '23 at 01:50Thread[{x, y}]Inner[List, x, y, List]– cvgmt Jan 30 '23 at 01:57