14

I have two lists.

list1 = {115.366, 103.583, 115.24, 91.4648, 93.1291, 485.744, 427.888,489.401, 403.942}

list2 = {114.062, 105.17, 114.857, 91.6497, 93.2112, 398.588, 458.713,410.015, 380.659}

I want these lists to form a table that looks like this. 

115.366    114.062
103.583    105.17
115.24     114.857
and so on
gwr
  • 13,452
  • 2
  • 47
  • 78
user2895279
  • 379
  • 1
  • 2
  • 7

6 Answers6

18
Transpose[{list1, list2}] // TableForm

$\begin{array}{cc} 115.366 & 114.062 \\ 103.583 & 105.17 \\ 115.24 & 114.857 \\ 91.4648 & 91.6497 \\ 93.1291 & 93.2112 \\ 485.744 & 398.588 \\ 427.888 & 458.713 \\ 489.401 & 410.015 \\ 403.942 & 380.659 \\ \end{array}$

David G. Stork
  • 41,180
  • 3
  • 34
  • 96
8

And then there is Grid:

transposedData = Transpose @ { list1, list2 }; (* make a list of tuples *)

Grid[
  transposedData,
  (* options for further formatting go here *)
]

Table

Just to give an idea of what is possible using options for Grid:

Grid[
  transposedData,
  Frame -> {All, None, {{3, 2} -> Directive[Red, Thick]}},
  Alignment -> {Decimal, Decimal}
]

nicer table

gwr
  • 13,452
  • 2
  • 47
  • 78
7

Although solution has been already accepted, here is another way it could be done

Example

Code

Row[(Column[#, Frame -> True] & /@ {list1, list2})]

Note: list1 and list2 as in OP

Output

output example

Reference

Map
Row
Column

e.doroskevic
  • 5,959
  • 1
  • 13
  • 32
4

Thanks to the @cvgmt's feedback, alternatives to Transpose:

Code 1

Thread[{list1, list2}]

% == Transpose[{list1, list2}]
(* Out: True *)

Code 2

Can only be used on two lists, each of them should be 1-dimensional:

Inner[List, list1, list2, List]

% == Transpose[{list1, list2}]
(* Out: True *)

Speed Comparison

lg[n_] := ConstantArray[RandomReal[{-1, 1}, 10^n], 2]

thread[{l1_, l2_}] := Thread[{l1, l2}];
inner[{l1_, l2_}] := Inner[List, l1, l2, List];
transpose[{l1_, l2_}] := Transpose[{l1, l2}];


Needs["GeneralUtilities`"]
BenchmarkPlot[{thread, inner, transpose}, lg, TimeConstrained -> 20]

Result:

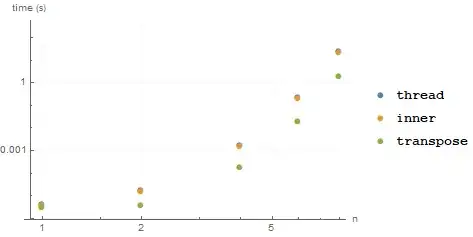
enter image description here

Ben Izd
  • 9,229
  • 1
  • 14
  • 45
  • Transpose is faster then others. list1 = RandomReal[{-1, 1}, 10^6]; list2 = RandomReal[{-1, 1}, 10^6]; Thread[List[list1, list2]]; // AbsoluteTiming Inner[List, list1, list2, List]; // AbsoluteTiming Transpose[List[list1, list2]]; // AbsoluteTiming – cvgmt Mar 25 '21 at 09:04
3

A new approach is based on the command ArrayReduce and it works in the following manner:

TableForm@ArrayReduce[Dot, {list1, list2}, 1]

Another alternative is based on the use of Multicolumn. It works like this:

Multicolumn[Flatten@ArrayReshape[{list1, list2}, {2, Length@list1}], 
   2]

In the above command, we can add at the end [[1]] // TableForm optionally. This will create a List and bring it into TableForm.

The output of the two commands above is

Blockquote

bmf
  • 15,157
  • 2
  • 26
  • 63
  • @user1066 very good points. Thanks for pointing those out. Indeed, ArrayReduce seems a very nice and useful gadget to have and I definitely need more practice with it :-) – bmf Feb 01 '23 at 01:27
0

Make your own function:

In[1]= myThread[l1__, l2__] := If[Length[l1] != Length[l2],"Error in length", {l1[[#]], l2[[#]]} & /@ Range[1, Length[l1]]]

list1 = Reverse[Range[1, 9]]
Out[1]= {9, 8, 7, 6, 5, 4, 3, 2, 1}


list1 = Range[1, 9]
Out[2]= {1, 2, 3, 4, 5, 6, 7, 8, 9}


In[2]= myThread[list1__, list2__]
Out[3]= {{9, 1}, {8, 2}, {7, 3}, {6, 4}, {5, 5}, {4, 6}, {3, 7}, {2, 8}, {1,9}}

You can expand the logic to any dimension. Also, applying //Tableform function at the end will format the output in the form you seek, viz.:

In[262]= list//TableForm
Out[263]//TableForm=
1    9
2    8
etc...
Ole SkoolNO
  • 1
  • 1