Keeping Nonlinear Model Fit Real

Question

So I am using the NonlinearModelFit (NLM) command with a fairly simple function. There are 4 unknowns and the (x, y) points that I am fitting the function to. I am getting my approximations from a Manipulate so I can just tweak the values till it's close enough. But once I get the values into the NLM, I get this error about the function value not being a real number at these values (not the same values that I put into the NLM). I have tried several different sets of values and every time I get the same error. I do have two constraints that keep two of my values positive.

R = 0.42; Sigma = 73.06967052; Theta=1.32757;

nData={{0.989939, 4.62}, {0.989939, 4.64}, {0.989939, 4.66},
       {0.989939, 4.68}, {0.989939, 4.7}, {0.989939, 4.72},
       {0.989939, 4.74}, {0.989939, 4.76}, {0.989939, 4.78},
       {0.989939, 4.8}, {0.99398, 4.82}, {0.99398, 4.84},
       {0.99398, 4.86}, {0.99398, 4.88}, {0.99398, 4.9},
       {0.99398, 4.92}, {0.99398, 4.94}, {0.99398, 4.96},
       {0.99398, 4.98}, {0.99398, 5}, {0.99398, 5.02},
       {0.99398, 5.04}, {0.99398, 5.06}, {0.99398, 5.08},
       {0.99398, 5.1}};

nlm = NonlinearModelFit[
    nData, 
    {((3 + s)/(1 + s) 1/R (h + dh)^(1 + s))* ((p/(Sigma*Cos[Theta]))^s)*
        Hypergeometric2F1[1 + s, s, 2 + s, (h + dh)/h0], s > 0, p > 0}, 
    {{p, 0.207}, {s, 1}, {h0, 2.04}, {dh, 0.9}}, h
 ]

R, sigma and theta are undefined. Could you also please provide a bit of data that has this problem? — Sjoerd C. de Vries, Jul 02 '13 at 17:48
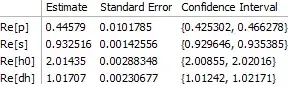
Short answer: after loading the package provided in this answer, use ComplexFit[..., "FitFunction" -> NonlinearModelFit, "CoordinateSystem" -> "Real"]. This has what might be considered some usability issues, but it will work. — Oleksandr R., Jul 03 '13 at 01:08
Oleksandr I am getting this error now.
NonlinearModelFit::optx: Unknown option FitFunction in NonlinearModelFit[nData,{((dh+h)^(1+s) (3+s) Hypergeometric2F1[s,1+s,2+s,(dh+h)/h0] ((p Sec[[Theta]])/[Sigma])^s)/(R (1+s)),s>0,p>0},{{p,0.207},{s,1},{h0,2.04},{dh,0.9}},{h},FitFunction->NonlinearModelFit,CoordinateSystem->Real]. >> — CouldntThinkOfAName, Jul 03 '13 at 13:27
Please re-read what I wrote. You have to use the package and function that I suggested, since this is something I implemented myself and not an option of NonlinearModelFit. — Oleksandr R., Jul 04 '13 at 18:24

score 2 · Answer 1 · edited Apr 13 '17 at 12:55

Your question is rather ill-formed as stated, because you have not included nData with enough precision and consequently many of the abscissae are duplicated.

Because I am confident that it will work regardless, to re-state what I said in a comment, you can do the following. First, load the TransformedFit/ComplexFit package I described here. Then, evaluate:

nlm = ComplexFit[nData, {
   ((3 + s)/(1 + s) 1/R (h + dh)^(1 + s))*
    ((p/(Sigma*Cos[Theta]))^s)*
    Hypergeometric2F1[1 + s, s, 2 + s, (h + dh)/h0],
   {TransformedParameter[Re, s] > 0, TransformedParameter[Re, p] > 0}
  }, {{p, 0.207}, {s, 1}, {h0, 2.04}, {dh, 0.9}}, h,
  "FitFunction" -> NonlinearModelFit, "CoordinateSystem" -> "Real"
 ];
nlm["ParameterConfidenceIntervalTable"]

Even with your incorrect data, no error messages are produced (except for one stating that the fit has not converged due to the aforementioned problem) and the result seems to be essentially reasonable:

NonlinearModelFit output with constraints

The constraints actually are not necessary any more. Without them, we get (far more quickly) a slightly different answer, due to a different method having been used by NonlinearModelFit:

NonlinearModelFit output without constraints

With the correct data, you are more likely to receive a unique and hopefully meaningful result. If this doesn't occur, you will need to experiment with the Method option. Any method supported by NonlinearModelFit can be used here, since ComplexFit merely transforms how the problem is stated before calling the usual fitting functions.

Keeping Nonlinear Model Fit Real

1 Answers1

Linked