NonlinearModelFit errors and precision

Question

For this problem, I use a data set, which I've made available here.

DataListTemp = Import["LED1_ext_I0_ 0.csv"];
DataList = Take[DataListTemp, {5, Length[DataListTemp]}];
CH1 = Table[DataList[[i, 2]]];
T = Table[DataList[[i, 1]]];
Data1 = Transpose[{T, CH1}];
ListPlot[Data1, PlotRange -> All, Joined -> True]

FWHM = 41.;
RiseTime = 15.;
FallTime = 34.;

UGLog[t_] := Umax Exp[-1/2 (Log[t/τ]/σ)^2] + A Exp[(t - μ)^2/γ]

FitCH1 = 
  NonlinearModelFit[Data1, ULog[t], 
   {{Umax, Min[CH1]}, 
    {τ,FWHM}, 
    {σ, RiseTime/FallTime},
    {A, Max[CH1]}, 
    {μ, T[[Flatten[Position[CH1,Max[CH1]]][[1]]]]}, 
    {γ, RiseTime/(5*FallTime)}}, 
    t,
    AccuracyGoal -> 30, 
    PrecisionGoal -> 30, 
    WorkingPrecision -> Automatic, 
    Method -> "Newton"]

From the plot of the data, I've noticed that there is an overshoot in the signal, which happens in all of my data sets. So I've included an extra Gaussian function term in my fit function to fit this part for a better fit. I've also tried playing around with the options for NonlinearModelFit, which resulted in nothing better. The actual errors I'm getting are:

The line search decreased the step size to within tolerance specified by AccuracyGoal and PrecisionGoal but was unable to find a sufficient decrease in the norm of the residual. You may need more than MachinePrecision digits of working precision to meet these tolerances_

and

The function value 6.43124*10^6+136628. I is not a real number at {Umax,[Tau],[Sigma]} = {-19.3669,-0.24269,-3.64767}

Can anyone help with these errors?

Your code contains basic syntax problems (unmatched brackets, etc) that prevent people from attempting your calculation. For instance, what do you mean by Table[DataList[[i,2]];? — MarcoB, Jun 29 '15 at 21:01
For the second problem, same answer applies as here. But, just like in the other case, your question is malformed, so it is not possible to help you with any additional specificity. — Oleksandr R., Jun 29 '15 at 23:39
I also strongly recommend you remove all of the unnecessary preprocessing code and just provide the data here in the form needed for NonlinearModelFit. — Oleksandr R., Jun 29 '15 at 23:42
I've edited the code as recommended. I thought about using the ComplexFit package, but none of my data should turn out complex. I've fit the data before and the only problem I had was a bad fit, but no complex number errors. — Karl, Jul 02 '15 at 13:45
Your question is reopened. If you do not want to use the ComplexFit package but still do not want complex numbers, then you should add a constraint to prevent these appearing, or give better initial guesses. — Oleksandr R., Jul 02 '15 at 22:28
It looks like you're trying to fit a curve that is a mixture of two normal distributions (as opposed to fitting a distribution from a random sample from a mixture of two normal distributions). Because the addition of the "extra Gaussian" is pretty ad hoc, I'm assuming/hoping that you're not considering comparing estimated coefficients among different datasets. Also, the data is very "discrete". The time values are exact multiples of the integers 1 through 1000 and the CH1 variable is a linear combination of the integers 0 through 100. Is a description of the data the objective? — JimB, Jul 03 '15 at 19:34
Oleksandr - After a second look at your complex fit package, I couldn't figure out how to import a package that wasn't implicit to Mathematica. How do I call it? If I don't use it, I wouldn't even know how to apply such a constraint. What would one look like?
Jim - The data is from an oscilloscope which was reading a PMT. I'm not sure if this answers your question. But yes, there are multiple data sets I wish to compare. — Karl, Jul 06 '15 at 16:21

score 2 · Answer 1 · edited Oct 06 '16 at 15:07

Here is how to get a fit to the curve form you give to the data set. Given the great deal of pattern in the data, it can be reproduced in a relatively compact form. And some of the pattern is a bit disconcerting in terms of the discreteness of the values and the way the time is recorded. There are 2 identical times repeated for "odd" times, and 3 identical times repeated for "even" times. Finally, I needed to remove the times that were zero because of the use of the Log function on time in the function.

(* Reproduce data from a compacted form *)
time = Flatten[Table[If[i == 1000, i, If[OddQ[i], {i, i}, {i, i, i}]], {i, 1000}]];
ch1Table = {{0, 3}, {1, 1}, {0, 14}, {1, 1}, {0, 3}, {1, 
   1}, {0, 2}, {1, 4}, {0, 3}, {1, 2}, {0, 4}, {1, 1}, {0, 3}, {1, 
   3}, {0, 22}, {1, 1}, {0, 14}, {1, 2}, {0, 3}, {1, 2}, {0, 5}, {1, 
   1}, {0, 3}, {1, 2}, {0, 4}, {1, 2}, {0, 2}, {1, 2}, {0, 12}, {1, 
   2}, {0, 4}, {1, 2}, {0, 14}, {1, 1}, {0, 2}, {1, 4}, {0, 2}, {1, 
   1}, {0, 5}, {1, 1}, {0, 3}, {1, 3}, {0, 1}, {1, 1}, {0, 1}, {1, 
   1}, {0, 8}, {1, 2}, {0, 7}, {1, 3}, {0, 18}, {1, 2}, {0, 2}, {1, 
   2}, {0, 8}, {1, 1}, {0, 4}, {1, 3}, {0, 2}, {1, 3}, {0, 14}, {1, 
   1}, {0, 8}, {1, 2}, {0, 9}, {1, 2}, {0, 1}, {1, 2}, {0, 14}, {1, 
   1}, {0, 3}, {1, 1}, {0, 6}, {1, 1}, {0, 9}, {1, 1}, {0, 2}, {1, 
   1}, {0, 16}, {1, 2}, {0, 1}, {1, 3}, {0, 4}, {1, 1}, {0, 12}, {1, 
   3}, {0, 2}, {1, 1}, {0, 11}, {1, 1}, {0, 2}, {1, 3}, {0, 18}, {1, 
   2}, {0, 2}, {1, 1}, {0, 10}, {1, 1}, {0, 3}, {1, 3}, {0, 3}, {1, 
   1}, {0, 14}, {1, 1}, {0, 3}, {1, 1}, {0, 15}, {1, 2}, {0, 3}, {1, 
   2}, {0, 8}, {1, 2}, {0, 4}, {1, 1}, {0, 18}, {1, 3}, {0, 22}, {1, 
   2}, {0, 3}, {1, 2}, {0, 8}, {1, 3}, {0, 1}, {1, 2}, {0, 3}, {1, 
   1}, {0, 4}, {1, 1}, {0, 10}, {1, 2}, {0, 2}, {1, 1}, {0, 14}, {1, 
   3}, {0, 3}, {1, 3}, {0, 3}, {1, 1}, {0, 8}, {1, 2}, {0, 2}, {1, 
   1}, {0, 31}, {1, 1}, {0, 3}, {1, 1}, {0, 3}, {1, 2}, {0, 14}, {1, 
   3}, {0, 1}, {1, 1}, {0, 6}, {1, 1}, {0, 4}, {1, 1}, {0, 7}, {1, 
   1}, {0, 1}, {1, 1}, {0, 17}, {1, 1}, {0, 1}, {1, 2}, {0, 8}, {1, 
   1}, {0, 13}, {1, 2}, {0, 12}, {1, 2}, {0, 20}, {1, 2}, {0, 1}, {1, 
   4}, {0, 1}, {1, 1}, {0, 10}, {1, 2}, {0, 2}, {1, 2}, {0, 4}, {1, 
   2}, {0, 3}, {1, 1}, {0, 24}, {1, 3}, {0, 2}, {1, 2}, {0, 7}, {1, 
   2}, {0, 4}, {1, 1}, {0, 3}, {1, 1}, {0, 1}, {1, 1}, {0, 2}, {1, 
   1}, {0, 16}, {1, 1}, {0, 4}, {1, 1}, {0, 14}, {1, 1}, {0, 3}, {1, 
   2}, {0, 3}, {1, 1}, {0, 4}, {1, 2}, {0, 2}, {1, 3}, {0, 2}, {1, 
   1}, {0, 4}, {1, 1}, {0, 4}, {1, 1}, {0, 10}, {1, 1}, {0, 14}, {1, 
   2}, {0, 3}, {1, 2}, {0, 3}, {1, 1}, {0, 4}, {1, 2}, {0, 7}, {1, 
   3}, {0, 18}, {1, 1}, {0, 13}, {1, 1}, {0, 4}, {1, 3}, {0, 2}, {1, 
   3}, {0, 11}, {1, 2}, {0, 1}, {1, 1}, {0, 8}, {1, 1}, {0, 25}, {1, 
   1}, {0, 2}, {1, 2}, {0, 2}, {1, 4}, {0, 3}, {1, 2}, {0, 8}, {1, 
   3}, {0, 1}, {1, 1}, {0, 1}, {1, 2}, {0, 12}, {1, 1}, {0, 3}, {1, 
   2}, {0, 15}, {1, 2}, {0, 1}, {1, 1}, {0, 1}, {1, 1}, {0, 13}, {1, 
   3}, {0, 1}, {1, 3}, {0, 5}, {1, 1}, {0, 3}, {1, 1}, {0, 47}, {1, 
   3}, {0, 3}, {1, 2}, {0, 3}, {1, 1}, {0, 9}, {1, 2}, {0, 19}, {1, 
   5}, {0, 1}, {1, 6}, {0, 1}, {1, 14}, {0, 2}, {1, 2}, {0, 2}, {1, 
   3}, {0, 4}, {1, 1}, {0, 3}, {1, 2}, {0, 4}, {1, 1}, {0, 6}, {1, 
   2}, {0, 1}, {1, 7}, {0, 3}, {1, 2}, {0, 1}, {1, 1}, {0, 4}, {1, 
   8}, {0, 2}, {1, 2}, {0, 3}, {1, 2}, {0, 4}, {1, 1}, {0, 1}, {1, 
   8}, {2, 4}, {3, 1}, {4, 1}, {5, 2}, {6, 1}, {7, 1}, {8, 1}, {9, 
   1}, {11, 1}, {12, 1}, {14, 1}, {16, 1}, {18, 1}, {20, 1}, {22, 
   1}, {24, 1}, {27, 1}, {29, 1}, {32, 1}, {35, 1}, {38, 1}, {41, 
   1}, {43, 1}, {46, 1}, {49, 1}, {52, 1}, {55, 1}, {58, 1}, {60, 
   1}, {63, 1}, {66, 1}, {69, 1}, {71, 1}, {73, 1}, {75, 1}, {77, 
   1}, {79, 1}, {81, 1}, {82, 1}, {84, 1}, {85, 1}, {87, 1}, {88, 
   1}, {89, 1}, {90, 1}, {91, 1}, {92, 1}, {93, 2}, {94, 1}, {95, 
   2}, {96, 3}, {97, 1}, {98, 9}, {99, 3}, {98, 3}, {99, 1}, {98, 
   3}, {97, 3}, {96, 2}, {95, 2}, {94, 2}, {93, 2}, {92, 1}, {91, 
   1}, {90, 2}, {89, 1}, {88, 1}, {87, 1}, {86, 1}, {85, 1}, {84, 
   1}, {83, 1}, {82, 1}, {80, 1}, {79, 1}, {78, 1}, {77, 1}, {76, 
   1}, {74, 1}, {73, 1}, {72, 1}, {71, 1}, {70, 1}, {68, 1}, {67, 
   1}, {66, 1}, {65, 1}, {64, 1}, {63, 1}, {62, 1}, {61, 1}, {60, 
   1}, {59, 1}, {58, 1}, {56, 2}, {55, 1}, {54, 1}, {52, 2}, {51, 
   1}, {50, 1}, {49, 1}, {48, 1}, {47, 2}, {46, 1}, {45, 1}, {44, 
   1}, {43, 1}, {42, 2}, {41, 1}, {40, 1}, {39, 1}, {38, 1}, {37, 
   1}, {36, 1}, {35, 1}, {34, 2}, {33, 1}, {32, 1}, {31, 1}, {30, 
   1}, {29, 1}, {28, 2}, {27, 1}, {26, 1}, {25, 1}, {24, 2}, {23, 
   1}, {22, 1}, {21, 1}, {20, 1}, {19, 1}, {18, 1}, {17, 2}, {16, 
   1}, {15, 1}, {14, 1}, {13, 2}, {12, 2}, {11, 2}, {10, 2}, {9, 
   2}, {8, 3}, {7, 1}, {6, 3}, {5, 2}, {4, 3}, {3, 2}, {2, 5}, {1, 
   4}, {0, 7}, {-1, 8}, {0, 1}, {-1, 17}, {0, 17}, {1, 23}, {2, 
   33}, {1, 8}, {2, 1}, {1, 3}, {2, 4}, {1, 6}, {2, 2}, {1, 3}, {2, 
   1}, {1, 4}, {2, 7}, {1, 13}, {2, 1}, {1, 16}, {2, 1}, {1, 3}, {2, 
   13}, {1, 1}, {2, 9}, {1, 1}, {2, 9}, {1, 1}, {2, 4}, {1, 1}, {2, 
   22}, {3, 2}, {2, 2}, {3, 3}, {2, 6}, {3, 27}, {4, 2}, {3, 1}, {4, 
   3}, {3, 2}, {4, 4}, {3, 1}, {4, 17}, {5, 1}, {4, 12}, {5, 4}, {4, 
   1}, {5, 1}, {4, 10}, {5, 1}, {4, 3}, {5, 3}, {4, 16}, {3, 1}, {4, 
   4}, {3, 1}, {4, 4}, {3, 1}, {4, 3}, {3, 4}, {4, 2}, {3, 2}, {4, 
   3}, {3, 1}, {4, 3}, {3, 25}, {2, 2}, {3, 4}, {2, 1}, {3, 25}, {4, 
   2}, {3, 29}, {4, 2}, {3, 2}, {4, 3}, {3, 1}, {4, 16}, {5, 2}, {4, 
   4}, {5, 2}, {4, 2}, {5, 2}, {4, 4}, {5, 5}, {4, 2}, {5, 1}, {4, 
   1}, {5, 39}, {4, 1}, {5, 4}, {4, 1}, {5, 2}, {4, 9}, {5, 1}, {4, 
   16}, {3, 3}, {4, 3}, {3, 1}, {4, 6}, {3, 1}, {4, 1}, {3, 2}, {4, 
   2}, {3, 4}, {4, 1}, {3, 55}, {4, 1}, {3, 13}, {4, 1}, {3, 72}, {2, 
   1}, {3, 14}, {2, 2}, {3, 3}, {2, 2}, {3, 1}, {2, 3}, {3, 3}, {2, 
   3}, {3, 3}, {2, 1}, {3, 3}, {2, 7}, {3, 3}, {2, 2}, {3, 4}, {2, 
   2}, {3, 1}, {2, 15}, {3, 1}, {2, 18}, {3, 1}, {2, 10}, {3, 1}, {2, 
   9}, {3, 1}, {2, 43}};
ch1 = Flatten[
   Table[Table[ch1Table[[i, 1]], {j, ch1Table[[i, 2]]}], {i, 
     Length[ch1Table]}]];
data = Table[{time[[i]]/100000000, -ch1[[i]]/250}, {i, Length[time]}];

(* Define function to fit *)
UGLog[t_] := Umax Exp[-1/2 (Log[t/τ]/σ)^2] + a Exp[(t - μ)^2/γ]

(* Find parameter estimates *)fitCH1 = 
 NonlinearModelFit[data, 
  UGLog[t], {{b, 0}, {Umax, -0.397}, {τ, 0.00000578}, {σ, 
    0.0252}, {a, -0.017}, {μ, 0.000008}, {γ, 0.000001}}, t,
   MaxIterations -> 300]

(* Show fit *)
Show[{ListPlot[data, PlotRange -> Full], 
  Plot[fitCH1[t], {t, 0.000001, 0.00001}, PlotRange -> Full, 
   PlotStyle -> Red]}, ImageSize -> Large]

(* Show residuals *)
ListPlot[fitCH1["FitResiduals"], ImageSize -> Large]

with the following results:

Fit

and the following residuals:

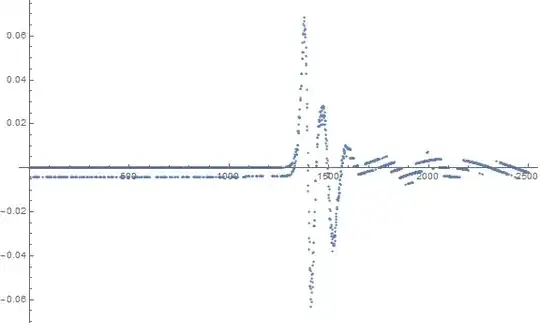
Residuals

The residuals have a great deal of pattern so I wouldn't call this a great fit.

The fit seems good enough. The discreteness of the values comes from using an oscilloscope with an 8-bit ADC apparently on the wrong gain setting, and the ringing is because of parasitic inductance in the measurement circuit. (Guesses on my part based on having seen similar things before. I cannot explain the strange time values.) — Oleksandr R., Sep 27 '15 at 00:01

NonlinearModelFit errors and precision

1 Answers1