Proving orthogonality of Hermite polynomials

Question

The orthogonality relation for Hermite polynomials is:

$$\int\limits_{-\infty}^\infty e^{-x^2} H_n(x) H_m(x)\ dx = 2^n n! \sqrt{\pi} \delta_{nm}$$

where $\{ n, m \} \in \mathbb{Z}_{\geq 0}$, $H_n(x)$ is the Hermite polynomial of order $n$, and $\delta_{nm}$ is the Kroneker delta indicator, which is $1$ if and only if $n=m$.

The straightforward approach does not work for arbitrary (but unspecified) $n$ and $m$:

Assuming[{n, m} ∈ NonNegativeIntegers,
 Integrate[
  E^(-x^2) HermiteH[n, x] HermiteH[m, x], 
  {x, -∞, ∞}]]

but will work for any specified such orders (see related question).

How can I computationally derive the orthogonality relation for arbitrary $n$ and $m$?

Answer 1

Since I got a thumbs up, I will present something. To the author of the OP, please let me know whether this is useful or not. If not, I am happy to delete it.

We begin by recording the Rodrigues' formula for the Hermite polynomials

$$ \begin{equation} H_n (x) = (-1)^n e^{x^2} \frac{d^n}{dx^n} \left( e^{-x^2} \right) \end{equation} $$

Using the above we can re-write the integral of interest as follows:

$$ \begin{equation} \int^{\infty}_{-\infty} ~ dx ~ e^{-x^2} ~ H_m(x) ~ H_n(x) = (-1)^n \int^{\infty}_{-\infty} ~ dx ~ H_m(x) ~ \frac{d^n}{dx^n} \left( e^{-x^2} \right) \end{equation} $$

And now we can separate two cases:

Case 1 We examine $m \neq n$. We will choose $m < n$ without loss of generality and integrate by parts to take all derivatives on the Hermite polynomial.

Assuming[{n, m} ∈ NonNegativeIntegers && m > n, 
 Integrate[
  D[HermiteH[m, x], {x, n}] Exp[-x^2], {x, -Infinity, Infinity}]]

Case 2 here we have $m=n$. Here, Mathematica provides us with the following

Assuming[{n} ∈ NonNegativeIntegers && n >= 0, 
 Integrate[
  D[HermiteH[n, x], {x, n}] Exp[-x^2], {x, -Infinity, Infinity}]]

The first bit is easy to see that is what we want, since

Factorial[n] == Gamma[1 + n] == FactorialPower[n, n] // FullSimplify

The thing that I have not understood as of yet, is why Mathematica is giving a 0. If I do

Integrate[
 D[HermiteH[0, x], {x, 0}] Exp[-x^2], {x, -Infinity, Infinity}]

I get

Edit thanks to @BobHanlon for reminding me.

With

res = Assuming[{n} ∈ NonNegativeIntegers && n >= 0, 
  Integrate[
   D[HermiteH[n, x], {x, n}] Exp[-x^2], {x, -Infinity, Infinity}]]

FunctionExpand will automatically convert FactorialPower to a Gamma.

Then, we can change the ComplexityFunction

gammatofac[expr_, n_] := 
  FullSimplify[expr, n ∈ Integers && n > 0, 
   ComplexityFunction -> ((LeafCount@# + 
        10 Count[#, _Gamma | _Pochhammer, {0, \[Infinity]}]) &)];

to convert the Gamma to a Factorial. Altogether it reads

gammatofac[Flatten[(res // FunctionExpand)[[1]]][[1]], n]

and returns

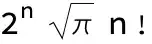
To the mathematicians: please do not hunt me down and kill for writing $\int dx ~ \texttt{stuff}$. We do it all the time in Physics.

Answer 2

Here us a simple analytical proof of the orthogonality of Hermite polynomials.

Physicists know well, that the Hermite functions are eigenfunctions of the harmonic oscillator. The Hermite function is:

psi[n,x]= Exp[-x^2/2] HermiteH[n,x]

where, for simplicity, I did not write the normalization factor. The Eigen equation reads:

(-d^2/dx^2 + x^2) psi[n,x] == (2n+1) psi[n,x]

Now, it is well know that Eigen functions to different Eigen values are orthogonal (matrix element of 2 different Eigen functions of the Eigen operator must be zero).

Answer 3

Surely you know this, and probably not fully addressing your question ...

 p[{n_, m_}] :=  Integrate[Exp[-x^2] 
                 HermiteH[n, x] HermiteH[m,x], {x, -\[Infinity], \[Infinity]}];
 Timing[Map[p, Tuples[{Range[10], Range[10]}]]]

returns:

That is, you can calculate the integral for any finite set, but it will take a long time.

It took 17 seconds to compute 100 of them on M1 chip!

Answer 4

I've never quite figured out an efficient way to apply MathematicalFunctionData to any problem. Often I cannot even figure out any way to apply it. The following shows some of the convolutions I feel are necessary for a simple table lookup:

orthoRule = Extract[
   MathematicalFunctionData["HermiteH:Polynomial", 
    "RelatedIdentities"],
   Position[
     ToExpression@ ToBoxes@ (*is this really necessary?*)
       MathematicalFunctionData["HermiteH:Polynomial", 
        "RelatedIdentities"],
     HoldPattern[Integrate[
       HermiteH[_, x_] HermiteH[_, x_] Power[
         Power[E, Power[x_, 2]], -1],
       {x_, _, _}]]
     ][[1, {1}]]] /.
  HoldPattern@Function[v_, Inactivate[a_ == b_]] :>
   RuleDelayed[
    Hold[a] /.
        Integrate -> Inactive[Integrate] /.
       Thread[v -> (Pattern[#, Blank[]] & /@ v)] /.
       \[FormalT] -> (x_) // ReleaseHold,
    b]
Inactivate[
  Integrate[
   E^(-x^2) HermiteH[n, x] HermiteH[m, x],
   {x, -[Infinity], [Infinity]}],
  Integrate] /. orthoRule
PiecewiseExpand[%, {n, m} [Element] NonNegativeIntegers] // Simplify

Some of the nutty things like ToExpression@ ToBoxes@... and Hold[a]... // ReleaseHold have to do with the evaluation and parsing of the integrand into a standard form. This was needed to construct a pattern that matched. The other constraint was blocking the evaluation of Integrate, which takes a long time just to return unevaluated.

Answer 5

You can also use the recursive formulas for the Hermite polynomials to proof the orthogonality property. Remember that $H_n'(t)=2nH_{n-1}(t)$ and $H_{n+1}(t)=2tH_n(t)-2nH_{n-1}(t)$

Then you can use partial integration to evaluate $$2(n+1)I_{n,m}=2(n+1)\int_{-\infty}^{\infty}H_n(t)H_m(t)e^{-t^2}dt=\int_{-\infty}^{\infty}H_{n+1}'(t)H_m(t)e^{-t^2}dt=\left[H_{n+1}(t)H_m(t)e^{-t^2}\right]_{-\infty}^{\infty}-\int_{-\infty}^{\infty}H_{n+1}\left(2mH_{m-1}(t)-2tH_m(t)\right)e^{-t^2}dt=\int_{-\infty}^{\infty}H_{n+1}(t)H_{m+1}(t)e^{-t^2}dt=I_{n+1,m+1}$$ Notice that the expression on the bottom is symmetrical, therefore we can conclude that $$2(n+1)I_{n,m}=2(m+1)I_{n,m}\ \forall n,m\in\mathbb{N}$$ and because $I_{n,m}$ is a convergent integral we can see that the Integral vanishes for $n\neq m$ and as a byproduct we obtained a recursive formula for the case of equality between n and m. With this recursion at hand and the gaussian error-integral we can inductively prove the orthogonality relation in all its glory.