4

I want to test a difficult integral : Integral on all reals of some complicated function involving the Hermitian polynomials, exponentials, squares, factorials, and being general considering any Hermitian polynomials. I know the answer (it's ridiculously short compared with the statement) and just wanted to check. But why Mathematica doesn't calculate my integral ? (I'm quite new on the system and don't understand what causes the trouble) :

Integrate[(HermiteH[n, x/a]*Exp[-x^2/(2 a^2)]/((n!)^(1/2) (Pi a^2)^(1/4)))^2*x^2,
          {x, -Infinity, Infinity}, 
          Assumptions :> {Element[n, Integers], Element[a, Reals], a > 0}]

And getting as a result:

Integrate[ x^2 Exp[-(x^2/(2 a^2))]^2 HermiteH[n, x/a]^2/(Sqrt[a^2] Sqrt[Pi] n!), 
           {x, -∞, ∞}, Assumptions :> {n ∈ Integers, a ∈ Reals, a > 0}]

What do I have to change to get an answer?

Artes
  • 57,212
  • 12
  • 157
  • 245
faero
  • 63
  • 3
  • 2
    Perhaps writing exp with a capital E will help? – Sjoerd C. de Vries Oct 20 '13 at 21:27
  • 2
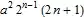
    Even after the correction in exp to Exp, it is not possible to get analytical solution. Mathematica graphics after about 3 minutes trying... also Maple 17 not able to do it. To help find such syntax errors, I always look at the equation for the green colored symbols (or is this blue colored? I always mix green with blue). If the symbol is not black colored, then it means Mathematica does not know about it. You could have seen that exp was green colored, this means Mathematica does know about it. – Nasser Oct 20 '13 at 21:41

2 Answers2

4

One can observe that given n Mathematica can evaluate the above integral symbolically assuming e.g. a > 0 (we needn't assume a ∈ Reals since the former assumption implies it). Thus finding e.g. the first 5 integrals we can make use FindSequenceFunction:

intherm[a_, n_] =
  FindSequenceFunction[ 
    Table[{n, Integrate[ E^(-x^2/a^2) x^2 HermiteH[n, x/a]^2/(n! Sqrt[(a^2)] Sqrt[π]), 
                         {x, -∞, ∞}, Assumptions -> a > 0]}, 
          {n, 0, 5}], n] // Simplify

 2^(-1 + n) a^2 (1 + 2 n)

TraditionalForm[2^(-1 + n) a^2 (1 + 2 n)]

enter image description here

Let's check the result for a large number n e.g. n = 131:

With[{n = 131}, 
     Integrate[(E^(-(x^2/a^2)) x^2 HermiteH[n, x/a]^2)/(n! Sqrt[(a^2)] Sqrt[π]), 
               {x, -∞, ∞}, Assumptions -> a > 0] == 2^(-1 + n) a^2 (1 + 2 n)]

True

There are different approaches e.g. exploiting recurrence relations between Hermite polynomials, but this one is quite simple and straightforward therefore there's no need for further considerations of the issue.

Artes
  • 57,212
  • 12
  • 157
  • 245
2

It is able to do the integration for fixed n.

hermInt[n_] := Integrate[(HermiteH[n, x/a]*
  Exp[-x^2/(2 a^2)]/((n!)^(1/2) (Pi a^2)^(1/4)))^2* x^2, {x, -Infinity, Infinity}, 
  Assumptions :> {Element[a, Reals], a > 0}]

Here are the first 10:

hermInt[#] & /@ Range[10]
{3 a^2, 10 a^2, 28 a^2, 72 a^2, 176 a^2, 416 a^2, 960 a^2, 2176 a^2, 4864 a^2, 10752 a^2}

If we look at these coefficients they form a nice pattern:

FindSequenceFunction[{3, 10, 28, 72, 176, 416, 960, 2176, 4864, 10752}, n]
2^(-1 + n) (1 + 2 n)
bill s
  • 68,936
  • 4
  • 101
  • 191