How do you calculate all the common tangents given two fixed circles and draw an image?

Question

The two fixed circle equations given are known to be:

x^2 + y^2 == 1
(x - 3)^2 + (y - 4)^2 == 16

By calculating that they have three common tangents

x==-1
5-3x-4y==0
25-7x+24y==0

Is there any way to calculate in Mathematica the tangent equations of the above two fixed circles and draw an image of the two circles and all the tangents?

I'm pretty sure the tangents aren't "male." Are you translating from some other language? — Michael E2, Feb 19 '23 at 14:05

cvgmt · Accepted Answer · 2023-02-20T10:56:43.260

The tangent line of the circle Circle[center,r] through the point {a,b} on circle and perpendicular to the direction {a,b}-center,so we set the tangent line to be

InfiniteLine[{a,b}, 
      RotationMatrix[π/2] . ({a, b} - center)]

We use RegionEqual to determint the common tangent lines, that is, if two tangent lines are coincident straight lines, then such two lines build a common tangent line.

Clear[c1, r1, c2, r2];
c1 = {0, 0};
r1 = 1;
c2 = {3, 4};
r2 = 4;
sol = Solve[{RegionEqual[
     InfiniteLine[{a1, b1}, 
      RotationMatrix[π/2] . ({a1, b1} - c1)], 
     InfiniteLine[{a2, b2}, 
      RotationMatrix[π/2] . ({a2, b2} - c2)]], {a1, 
      b1} ∈ Circle[c1, r1], {a2, b2} ∈ 
     Circle[c2, r2]}, {a1, b1, a2, b2}, Reals];
graphs = 
 Graphics[{Red, Point[{{a1, b1}, {a2, b2}}], Circle[c1, r1], 
      Circle[c2, r2], RandomColor[], AbsoluteThickness[2], 
      InfiniteLine[{a1, b1}, 
       RotationMatrix[π/2] . ({a1, b1} - c1)], , 
      InfiniteLine[{a2, b2}, 
       RotationMatrix[π/2] . ({a2, b2} - c2)]}] /. # & /@ sol
Show[graphs, Axes -> True, AxesStyle -> Arrowheads[{0.05}]]

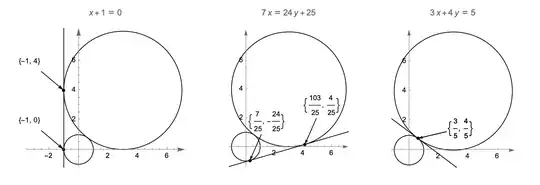
Convert the lines to the implicit form.

RegionConvert[
     InfiniteLine[{a1, b1}, 
       RotationMatrix[π/2] . ({a1, b1} - c1)] /. #, 
     "Implicit"][[1]] /. {\[FormalX] -> x, \[FormalY] -> y} & /@ sol

{1 + x == 0, 7 x == 25 + 24 y, 3 x + 4 y == 5}

Test random circles.

Clear["Global`*"];
tangentLines[{{x1_, y1_}, r1_}, {{x2_, y2_}, r2_}] := 
 Module[{sol, graph},
  sol = Solve[{RegionEqual[
       InfiniteLine[{a1, b1}, 
        RotationMatrix[π/2] . ({a1, b1} - {x1, y1})], 
       InfiniteLine[{a2, b2}, 
        RotationMatrix[π/2] . ({a2, b2} - {x2, y2})]], {a1, 
        b1} ∈ Circle[{x1, y1}, r1], {a2, b2} ∈ 
       Circle[{x2, y2}, r2]} // Rationalize[#, 0] &, {a1, b1, a2, b2},
     Reals];
  If[sol=={}, 
   Graphics[{Red, Circle[{x1, y1}, r1], Circle[{x2, y2}, r2]}], 
   Graphics[{Red, Point[{{a1, b1}, {a2, b2}}], Circle[{x1, y1}, r1], 
        Circle[{x2, y2}, r2], RandomColor[], AbsoluteThickness[2], 
        InfiniteLine[{a1, b1}, 
         RotationMatrix[π/2] . ({a1, b1} - {x1, y1})], , 
        InfiniteLine[{a2, b2}, 
         RotationMatrix[π/2] . ({a2, b2} - {x2, y2})]}] /. # & /@ 
    sol]]
SeedRandom[1];
ListAnimate[Table[({x1, y1} = RandomReal[{-4, 4}, 2];
   {x2, y2} = RandomReal[{-4, 4}, 2];
   r1 = RandomReal[{0, 4}];
   r2 = RandomReal[{0, 4}];
   tangentLines[{{x1, y1}, r1}, {{x2, y2}, r2}] // 
    Show[#, Axes -> True, AxesStyle -> Arrowheads[{0.05}]] &), {i, 
   20}], AnimationRate -> 1]

It's really too powerful. Can you add a planar Cartesian coordinate system? — csn899, Feb 19 '23 at 09:13
Does this code adapt to any two circles finding their male tangents? — csn899, Feb 19 '23 at 09:19
Can you add arrows to the right and up of the x-axis and y-axis respectively? — csn899, Feb 19 '23 at 09:26
@csn899 Yes, we can change the value of c1, r1, c2, r2 for any two circles. — cvgmt, Feb 19 '23 at 09:30
Can you calculate and display the straight-line equations for all the common tangents? — csn899, Feb 19 '23 at 09:48
The code of random circles.Can this code add dynamic common tangent equation? — csn899, Feb 20 '23 at 02:01
@csn899 Yes,it is easy done, but I think it make the pictures too complex. — cvgmt, Feb 20 '23 at 02:09
The line equation can be displayed in the upper right corner of the picture, and the corresponding line and equation are represented in the same color. — csn899, Feb 20 '23 at 02:11

kirma · Answer 2 · 2023-02-19T12:47:32.420

This solution is a little bit... elaborate for the task, but shows how one can use GeometricTest to find solutions using synthetic geometry tools:

With[
  {c1 = {0, 0}, r1 = 1,
   c2 = {3, 4}, r2 = 4,
   pts = {p1 -> {x1, y1}, p2 -> {x2, y2}, v -> {vx, vy}}},
  With[{sol =
     Solve[
      {(* Point p1 lies on first circle, and the circle and line
          passing through this point to the direction v are tangent. *)
        GeometricTest[
         {CircleThrough[{p1}, c1, r1],
          InfiniteLine[p1, v]},
         "Tangent"],
        (* Point p2 lies on second circle, and the circle and line
           passing through this point to the direction v are tangent. *)
        GeometricTest[
         {CircleThrough[{p2}, c2, r2],
          InfiniteLine[p2, v]},
         "Tangent"],
        (* Point p2 is on the line *)
        (* This is actually a workaround for bug in RegionMember
           with a non-constant InfiniteLine. *)
        Quiet@RegionDistance[InfiniteLine[p1, v], p2] == 0,
        (* v is of unit length *)
        Norm[v] == 1,
        (* Prevent finding mirror images of v. *)
        vx > 0 || (vx == 0 && vy > 0)} /. pts,
      Flatten[{p1, p2, v} /. pts], Reals]},
   Graphics[
       {Circle[c1, r1], Circle[c2, r2],
         InfiniteLine[p1, v],
         PointSize[Medium],
         Point[{p1, p2}],
         With[{off = RotationTransform[50 Degree][v]},
              {Arrow[{# + 2 off, #}], Text[#, # + 3 off]}] & /@
            {p1, p2}} /. pts,
       ImagePadding -> 15,
       Axes -> True, AxesStyle -> Arrowheads[{0.05}],
       PlotLabel ->
        (* Solve line equation. *)
        TraditionalForm@Refine[
          RegionMember[
           InfiniteLine[p1, v] /. pts /. #, {x, y}],
          Element[Alternatives[x, y], Reals]]] /. # & /@ sol]] //
 GraphicsRow[#, ImageSize -> 768] &

Show[graphs, Axes -> True, AxesStyle -> Arrowheads[{0.05}]Why didn't I show axes and arrows when I added this? — csn899, Feb 19 '23 at 10:35
This code is also very good. Can the coordinates of the tangent points in each graph be calculated and marked next to the tangent points in each diagram. — csn899, Feb 19 '23 at 11:00
Thank you very much! Can this code adapt to any given two fixed circles to find their common tangent and tangent coordinates? — csn899, Feb 19 '23 at 22:52
@csn899 You can try, but I found out that some parts of the GeometricTest functionality may be a bit fragile in cases where circles are tangent to each other for tangent line between them. Technically InfiniteLine direction vector form is not mentioned in the documentation for this... — kirma, Feb 19 '23 at 23:17

How do you calculate all the common tangents given two fixed circles and draw an image?

2 Answers2