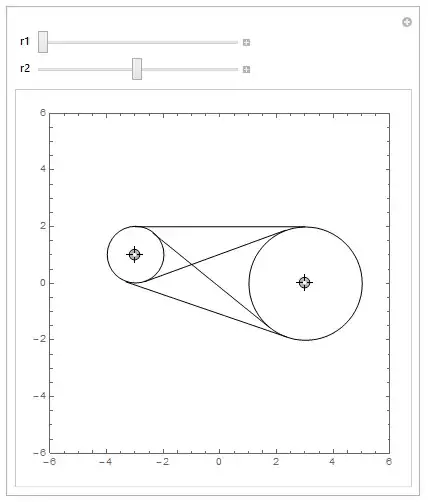
I have code worked for drawing common tangent lines to two circles(http://en.wikipedia.org/wiki/Tangent_lines_to_circles), now I want to delete the inner common tangent lines, how?
Manipulate[Block[{t1, t2, v1, v2, pts},
t1 = {xm, ym};
t2 = {xn, yn};
{v1, v2} = p;
pts = {t1, t2} /. NSolve[{(t2 - v2).(t2 - t1) == 0, (t1 - v1).(t2 - t1) == 0,
(t1 - v1).(t1 - v1) == r1^2, (t2 - v2).(t2 - v2) == r2^2}, {xm, ym, xn, yn}, Reals];
If[pts == {t1, t2}, pts = {}];
Graphics[{Circle[v1, r1], Circle[v2, r2], Line[pts]},
PlotRange -> 6, Frame -> 1]
], {{p, {{-3, 1}, {3, 0}}}, Locator}, {{r1, 1}, 1, 3}, {{r2, 2}, 1,
3}]





(t1 - v1).(t2 - v2) > 0in the equation system. – C. E. Aug 23 '14 at 11:54