Helfrich model is a set of non-linear differential equations in physics that are used to determine the shape of a biological cell given pressure differential dP (inside and outside the cell) and thermodynamic tension LK. It was first successfully used to explain the biconcave shape of red blood cells.
I have a custom built code (written by someone else) that solves the equations but I am wondering if there is an easy way to take advantage of the built-in functionality of NDSolve to get similar result? Below I mention the algorithm that solves the equation and provide the custom code.
(*algorithm : solving the helfrich eqns *)
equations for dependent variable are f'[s], c'[s] and d'[s] are provided. s is the independent variable;
c'=(-2 dSqrt[1 - f c^2])/f;
f'=4Sqrt[1 - f c^2];
d'=-(2c^2(d-c0)+c(c0^2-d^2)+LK c +dP + 4 d(1-f c^2)/f)/Sqrt[1 - f c^2];
we are solving them below with a combination of RK4 and Newton method (ensuring the boundary conditions are satisfied).
Detailed Procedure:
we assume dP=17.48 and c0 = -4;
(1) take some arbitrary initial test values where x -> c[0], y -> c[0.5], z -> d[0.5] and [Beta], a flag set to True;
(2) while [Beta] remains true:
Compute thermodynamic tension LK. This is computed at s = 0.5 for convenience.
LK = 2 y (c0-z)+z^2-c0^2-(dP/y);
Feed the 3 eqns (eqn1,eqn2,eqn3) to sisRK4 ---> c with value x, f with value 0.001, d with
value 0.0 and s with value 0.0 and 0.5; (see code below)
sisRK4 will compute updated values for c,f and d;
(3) obtain new values of c, f and d at s = 0.5 i.e. cN,fN and dN and compare values with the boundary condition.
The comparisons are f1,f2,f3.
f1=Abs[y*Sqrt[fN]-1];
f2=Abs[y-cN];
f3=Abs[z-dN];
(4) if these values agree with the BCs to a defined tolerance then we have the solution Sol.
else we apply the newton's method:
we sequentially increase x, y and z by a small amount hx, hy, hz and compute new LK and RK4
to find estimates of c,f and d at 0.5 .. new error estimates {f1x,f2x,f3x}, {f1y,f2y,f3y}, {f1z,f2z,f3z} are made
and derivatives of error are computed from (f1x - f1)/hx etc to from the Jacobian matrix. From the inverse of
Jacobian matrix and error vector {f1,f2,f3} new test values are determined by using:
{x,y,z} = {x,y,z} - Inverse[Jacobian].{f1,f2,f3}
Procedure is repeated until convergence is achieved within a specified tolerance.
*)
The code for the procedure above is provided as follows:
(*the function sisRK4 integrates equations using RK4*)
sisRK4[{p_, q_, r_}, {s_, s0_, sn_}, {c_, c0_}, {f_, f0_}, {d_, d0_},
steps_] := Block[{sold = s0, cold = c0, fold = f0, dold = d0,
sollist = {{s0, c0, f0, d0}}, s, c, f, d, h},
h = N[(sn - s0)/steps];
Do[
rule = {s -> sold, c -> cold, f -> fold, d -> dold};
snew = sold + h;
k1 = h (p /. rule);
l1 = h (q /. rule);
m1 = h (r /. rule);
rule = {s -> sold + h/2., c -> cold + k1/2., f -> fold + l1/2.,
d -> dold + m1/2.};
k2 = h (p /. rule);
l2 = h (q /. rule);
m2 = h (r /. rule);
rule = {s -> sold + h/2., c -> cold + k2/2., f -> fold + l2/2.,
d -> dold + m2/2.};
k3 = h (p /. rule);
l3 = h (q /. rule);
m3 = h (r /. rule);
rule = {s -> sold + h, c -> cold + k3, f -> fold + l3,
d -> dold + m3};
k4 = h (p /. rule);
l4 = h (q /. rule);
m4 = h (r /. rule);
cnew = cold + (1/6.) (k1 + 2 k2 + 2 k3 + k4);
fnew = fold + (1/6.) (l1 + 2 l2 + 2 l3 + l4);
dnew = dold + (1/6.) (m1 + 2 m2 + 2 m3 + m4);
AppendTo[sollist, {snew, cnew, fnew, dnew}];
sold = snew;
cold = cnew;
fold = fnew;
dold = dnew,
steps
];
sollist
];
ClearAll[s, c, f, d, h];
c0 = -4.0;
dP = 17.48;
(*initial test values*)
x = -0.8;
y = 0.8;
z = -0.6;
\[Beta] = True;
While[[Beta],
LK = 2 y (c0 - z) + z^2 - c0^2 - (dP/y);
Sol = sisRK4[{c' = (-2 d Sqrt[1 - f c^2])/f, f' = 4 Sqrt[1 - f c^2],
d' = -(2 c^2 (d - c0) + c (c0^2 - d^2) + LK c + dP +
4 d (1 - f c^2)/f)/Sqrt[1 - f c^2]}, {s, 0.0, 0.5}, {c,
x}, {f, 0.001}, {d, 0.0}, 1000];
(obtained values at s=0.5 )
cN = Sol[[1001, 2]];
fN = Sol[[1001, 3]];
dN = Sol[[1001, 4]];
(checking for the boundary conditions)
f1 = Abs[y*Sqrt[fN] - 1];
f2 = Abs[y - cN];
f3 = Abs[z - dN];
[Beta] = If[f1 < 0.001 && f2 < 0.001 && f3 < 0.001, False, True];
(application of Newton Method)
If[[Beta],
(partial derivatives in x)
hx = 0.001;
x2 = x + hx;
LK = 2 y (c0 - z) + z^2 - c0^2 - (dP/y);
Sol =
sisRK4[{c' = (-2 d Sqrt[1 - f c^2])/f, f' = 4 Sqrt[1 - f c^2],
d' = -(2 c^2 (d - c0) + c (c0^2 - d^2) + LK c + dP +
4 d (1 - f c^2)/f)/Sqrt[1 - f c^2]}, {s, 0.0, 0.5}, {c,
x2}, {f, 0.001}, {d, 0.0}, 1000];
cNx = Sol[[1001, 2]];
fNx = Sol[[1001, 3]];
dNx = Sol[[1001, 4]];
f1x = Abs[y*Sqrt[fNx] - 1];
f2x = Abs[y - cNx];
f3x = Abs[z - dNx];
(partial derivatives in y)
hy = 0.001;
y2 = y + hy;
LK = 2 y2 (c0 - z) + z^2 - c0^2 - (dP/y2);
Sol =
sisRK4[{c' = (-2 d Sqrt[1 - f c^2])/f, f' = 4 Sqrt[1 - f c^2],
d' = -(2 c^2 (d - c0) + c (c0^2 - d^2) + LK c + dP +
4 d (1 - f c^2)/f)/Sqrt[1 - f c^2]}, {s, 0.0, 0.5}, {c,
x}, {f, 0.001}, {d, 0.0}, 1000];
cNy = Sol[[1001, 2]];
fNy = Sol[[1001, 3]];
dNy = Sol[[1001, 4]];
f1y = Abs[y2*Sqrt[fNy] - 1];
f2y = Abs[y2 - cNy];
f3y = Abs[z - dNy];
(partial derivatives in z)
hz = 0.001;
z2 = z + hz;
LK = 2 y (c0 - z2) + z2^2 - c0^2 - (dP/y);
Sol =
sisRK4[{c' = (-2 d Sqrt[1 - f c^2])/f, f' = 4 Sqrt[1 - f c^2],
d' = -(2 c^2 (d - c0) + c (c0^2 - d^2) + LK c + dP +
4 d (1 - f c^2)/f)/Sqrt[1 - f c^2]}, {s, 0.0, 0.5}, {c,
x}, {f, 0.001}, {d, 0.0}, 1000];
cNz = Sol[[1001, 2]];
fNz = Sol[[1001, 3]];
dNz = Sol[[1001, 4]];
f1z = Abs[y*Sqrt[fNz] - 1];
f2z = Abs[y - cNz];
f3z = Abs[z2 - dNz];
(constructing the Jacobian Matrix)
Jf = ( {
{(f1x - f1)/hx, (f1y - f1)/hy, (f1z - f1)/hz},
{(f2x - f2)/hx, (f2y - f2)/hy, (f2z - f2)/hz},
{(f3x - f3)/hx, (f3y - f3)/hy, (f3z - f3)/hz}
} );
Vectorf = {f1, f2, f3};
Vectorx = {x, y, z};
Vectorx2 = Vectorx - Inverse[Jf] . Vectorf;
(* New test values)
{x, y, z} = Vectorx2;
];
];
(creating matrices that represent c,f and d as a function of S*)
cvar = Sol[[All, {1, 2}]];
fvar = Sol[[All, {1, 3}]];
dvar = Sol[[All, {1, 4}]];
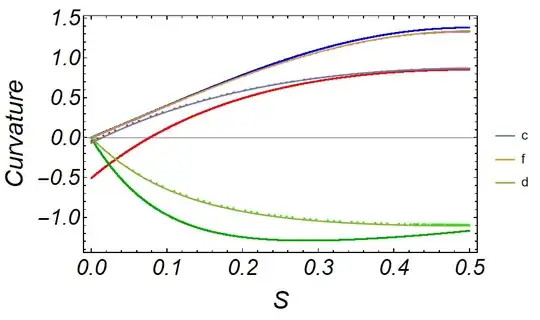
(Plotting the curvatures)
plotcurvatures =
ListPlot[{cvar, fvar, dvar}, PlotRange -> Full,
PlotLegends -> {"c", "f", "d"}, Frame -> True,
FrameLabel -> {Text[Style["S", 25, Italic]],
Text[Style["Curvature", 25, Italic]]},
FrameStyle -> Directive[Thickness[0.0025], Black, Italic],
FrameTicksStyle -> Directive[Black, 22],
PlotStyle -> {Red, Blue, Darker@Green}, AspectRatio -> 0.6,
ImageSize -> 600]




NDSolve? From this explanation it looks likeLK == 2 c[0.5] (c0 - d[0.5]) + d[0.5]^2 - c0^2 - (dP/c[0.5]),c[0.5] Sqrt[f[0.5]] == 1, f[0]==10^-3, d[0]==0. Is it correct? – Alex Trounev Feb 25 '23 at 03:24d[s]=0, c[s]=1,f[s]=(1 + 120 Sqrt[1110] s - 4000 s^2)/1000. – Alex Trounev Feb 25 '23 at 06:01NDSolveto find solution to the set of equations more conveniently than the custom code. Maybe a combination of NDSolve and FindRoot. What do you think? – Ali Hashmi Feb 25 '23 at 07:50dPis used. Here I just fixed it to 17.48 – Ali Hashmi Feb 25 '23 at 07:53