Given the following problem $$u_{tt}-\frac{v}{2}\cdot u_{xx}+\frac{v}{2}\cdot x^2 \cdot u(x)=0 $$ $$u(x,0)=f(x)$$ $$u_t(x,0)=g(x)=0$$ Where $ f(x)=y_0(x) $
$y_n$ are the Eigenfunctions that defined as $ y_n(x)=\exp\left(\displaystyle{\frac{-x^2}{2}}\right)H_n(x) $
By separation we assume $$u(x,t)=X(x)T(t)$$
$$\frac{T''(t)}{T(t)}=v (\frac{1}{2} \frac{X''(x)}{X(x)}-\frac{x^2}{2})=-\lambda$$
So we have
$$T''(x)=-\lambda v T(x)$$
I have found that the general solution of $T$ is
$T(x)=c_1 \cos{\sqrt{\lambda v}t}+c_2 \sin{\sqrt{\lambda v}t}$
and for $$\frac{1}{2} \frac{X''(x)}{X(x)}-\frac{x^2}{2}=-\lambda$$ which gives $$-\frac{1}{2}X''(x)+\frac{x^2}{2}X(x)=\lambda X(x)$$
the general solution of $X$ is $ X_n(x)=\exp\left(\displaystyle{\frac{-x^2}{2}}\right)H_n(x) $ given by our textbook and the eigenvalues are $\lambda_n=n+\frac{1}{2}$
So the general solution to our initial problem is $u_n(x,t)=\sum_{n=1}^{\infty} (A_n \cos{\sqrt{\lambda v}t}+B_n \sin{\sqrt{\lambda v}t}) \exp\left(\displaystyle{\frac{-x^2}{2}}\right)H_n(x)$
Using the I.C we got $$ u(x,0)=\sum_{n=1}^{\infty}A_n \exp\left(\displaystyle{\frac{-x^2}{2}}\right)H_n(x)=f(x) $$ To finish our solution, we need to solve the equation for the $A_n.$
To do this, you need to use the orthogonality property of Hermite polynomials: $$A_n=\frac{1}{\sqrt{2\pi}n!} \int_{-\infty}^\infty u(x,0) H_n(x) e^{-x^2/2} dx $$
I have solved this problem numerically with the following code
Her[n_] := HermiteH[n, x]
Y[n_] := Exp[-x^2/2]*Her[n]
Y[0]
f[x_] = Y[0]
PDE = \!\(
\*SubscriptBox[\(\[PartialD]\), \(t, t\)]\(V[x, t]\)\) - 1/2 \!\(
\*SubscriptBox[\(\[PartialD]\), \({x, 2}\)]\(V[x, t]\)\) +
1/2*x^2*V[x, t] == 0
BCs = {u[-21, t] == 0, u[21, t] == 0}
IC = u[x, 0] == f[x]
IC2 = \!\(
\*SubscriptBox[\(\[PartialD]\), \(t\)]\(u[x, 0]\)\) == 0
sol =
V /. First[NDSolve[{\!\(
\*SubscriptBox[\(\[PartialD]\), \(t, t\)]\(V[x, t]\)\) - 1/2 \!\(
\*SubscriptBox[\(\[PartialD]\), \({x, 2}\)]\(V[x, t]\)\) +
1/2*x^2*V[x, t] == 0, V[x, 0] == f[x],
\!\(\*SuperscriptBox[\(V\),
TagBox[
RowBox[{"(",
RowBox[{"0", ",", "1"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, 0] == 0,
V[-21, t] == V[21, t] == 0}, {V}, {t, 0, 20}, {x, -21, 21},
MaxStepSize -> 100000, MaxSteps -> 100000, PrecisionGoal -> 4]]
fig2 = Plot3D[sol[x, t], {t, 0, 10}, {x, -21, 21}, PlotRange -> All,
ColorFunction -> (ColorData[{"DeepSeaColors", "Reverse"}][#3] &)]
fig4 = Plot[sol[x, 3], {x, -21, 21}, PlotRange -> All,
PlotStyle -> {{RGBColor[1, 0, 0], Dashed, Thick}}]
Now I have tried to solve it analytically but the following code gave no results! Any suggestions?
Clear["Global`*"]
Her[n_] := HermiteH[n, x]
Y[n_] := Exp[-x^2/2]*Her[n]
Y[0]
f[x_] = Y[0]
IC = u[x, 0] == f[x]
IC2 = \!\(
\*SubscriptBox[\(\[PartialD]\), \(t\)]\(u[x, 0]\)\) == 0
v = 1
\[Omega] = Sqrt[\[Lambda]*v]
U[x_, t_, N_] = \!\(
\*UnderoverscriptBox[\(\[Sum]\), \(n =
1\), \(N\)]\(\((a[n]*Cos[\[Omega]*t] + b[n]*Sin[\[Omega]*t])\)*
HermiteH[n, x]*Exp[\(-x^2\)/2]\)\)
integrand[n_] = f[x]*HermiteH[n, x]*Exp[-x^2/2]/Sqrt[2 Pi*n!]
A[n_] = NIntegrate[integrand[n], {x, -Infinity, Infinity}]
u[x_, t_] = U[x, t, 10]
fig1 = Plot3D[u[x, t], {t, 0, 10}, {x, -21, 21}, PlotRange -> All,
ColorFunction -> "BlueGreenYellow"]
fig3 = Plot[u[x, 3], {x, 0, Pi}, PlotRange -> All,
PlotStyle -> {{RGBColor[0, 0, 1], AbsoluteThickness[0.5`]}}]

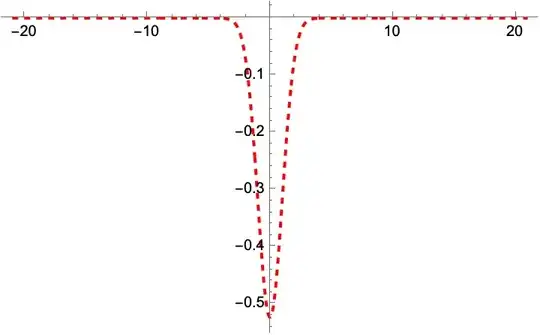
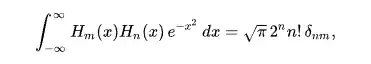


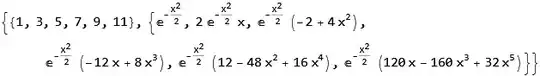
NDEigenvaluesand they do not agree. You can check and see for yourself.DEigenvaluescan not solve them analytically as per last question. Does the book show how they found them? There is something off somewhere. The first 6 eigenvalues I get are{0.53174, 1.53811, 2.84577, 4.1346, 5.26635, 7.19663}– Nasser Mar 28 '23 at 21:58DEigenvalues(i.e. analytically) and they match the book. Will try to write something. – Nasser Mar 28 '23 at 22:34Nfor variables in your code. This is builtin symbol. Also then!should not be inside the sqrt, it is outside. See Wikpedia. https://en.wikipedia.org/wiki/Hermite_polynomials – Nasser Mar 29 '23 at 01:14