I am working with finite difference methods analytically and I would like to be able to perform operations on subscripted variables.
I would like to generate the following expression by applying a central difference function to a variable twice: $$\frac{y_{i+1} - 2 y_i + y_{i-1}}{\Delta x^2}$$
I have written the function:
CentralDiff[var_, i_] := (Subscript[var, i + 1] - Subscript[var, i - 1])/(
2 Δx)
With this I can do the first derivative:
CentralDiff[y, 0]
Which returns: (-Subscript[y, -1] + Subscript[y, 1])/(2 Δx) The subscripts are correct.
If I try to get the 2nd derivative the :
CentralDiff[CentralDiff[y, 0], 0]
(*
(-Subscript[((-Subscript[y, -1] + Subscript[y, 1])/(2 Δx)), -1] +
Subscript[(-Subscript[y, -1] + Subscript[y, 1])/(2 Δx), 1])/(2 Δx)
*)
For the 2nd derivative using central differences the subscripts are not updated. I think I would have to define an operator for the subscripts perhaps? I don't know where to start with this. Perhaps there's an easier way?




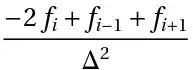

DifferenceQuotient[f[x - \[CapitalDelta]], {x, 2, \[CapitalDelta]}]? – kglr May 18 '23 at 13:06