5

I wish to detect the existence of a periodic orbit (limit cycle). For example, the test should return FALSE (i.e. it should fail) for the left (m = 0.35) and return TRUE for the right (m = 0.3) in the following toy model.

sys[m_] := {
  x'[t] == x[t] - 0.5 x[t]^2 - x[t] y[t] (x[t] - 1)  / (x[t]^2 - 1),
  y'[t] == -m y[t] +  x[t] y[t] (x[t] - 1) / (x[t]^2 - 1),
  x[0] == 0.1,
  y[0] == 0.1}

T = 500;


m = 0.35;
sol = First[NDSolve[{sys[m]}, {x, y}, {t, 0, T}]];
p = Plot[Evaluate[{x[t], y[t]} /. sol], {t, 0, T}];


m = 0.3;
sol2 = First[NDSolve[{sys[m]}, {x, y}, {t, 0, T}]];
p2 = Plot[Evaluate[{x[t], y[t]} /. sol2], {t, 0, T}];


GraphicsRow[{p, p2}]

m=0.35 on left, m=0.3 on right

Note that I am not interested in performing local stability analysis on the system (with which the Hopf bifurcation of the above toy model could be discerned), but rather wish to assess the existence of an orbit from the numerical solution itself.

It seems that using a Poincaré section and WhenEvent is the way to go, but I have not figured out a way to implement it that is robust to short transients (when x'[t]==0 is true for all t in the evaluated time period, an empty solution is returned) or very long transients, as demonstrated in the following by changing the period of time (Tstart to Tend) that is assessed:

test[m_] :=
 Module[{res},
  res = Reap[nd[{m}] =
      NDSolve[{sys[m], 
        WhenEvent[x'[t] == 0 && t > Tstart, 
         Sow[{m, Round[y[t], 10^-5]}]]},
       {x[t], y[t]},
       {t, 0, Tend},
       MaxSteps -> \[Infinity]]][[-1, 1]];
  CountDistinct[res] == 2
  ]

(* "Correct" inference *)

Tstart = 4500;
Tend = 5000;
test[0.35]
test[0.3]


Out[2916]= False


Out[2917]= True

(* False negative for m=0.3; still in transient phase *)

Tstart = 450;
Tend = 500;
test[0.35]
test[0.3]

Out[2920]= False

Out[2921]= False

(* non-existent part for m=0.35 when past transient phase *)

Tstart = 45000;
Tend = 50000;
test[0.35]
test[0.3]

During evaluation of In[2922]:= Part::partw: Part 1 of {} does not exist.

During evaluation of In[2922]:= Part::partw: Part 1 of {} does not exist.

Out[2924]= False

Out[2925]= True

I have not managed to make sense of How to locate the position of a periodic orbit and Locating periodic orbits with Mathematica.

user12734
  • 349
  • 1
  • 7

4 Answers4

3

Try

{X, Y} = NDSolveValue[{sys[m]}, {x, y}, {t, 0, T}]

Assuming periodoc solution near t~T the period tp follows with

gz=NMinimize[{  (X[T] - X[T-tp ])^2 + (Y[T] - Y[T-tp ])^2, 1 < tp < 20  }, tp ]
(* {7.54119*10^-12, {tp -> 16.2574}}*)

ParametricPlot[ {X[t], Y[t]}  , {t, T - tp /. gz[[2]], T}]

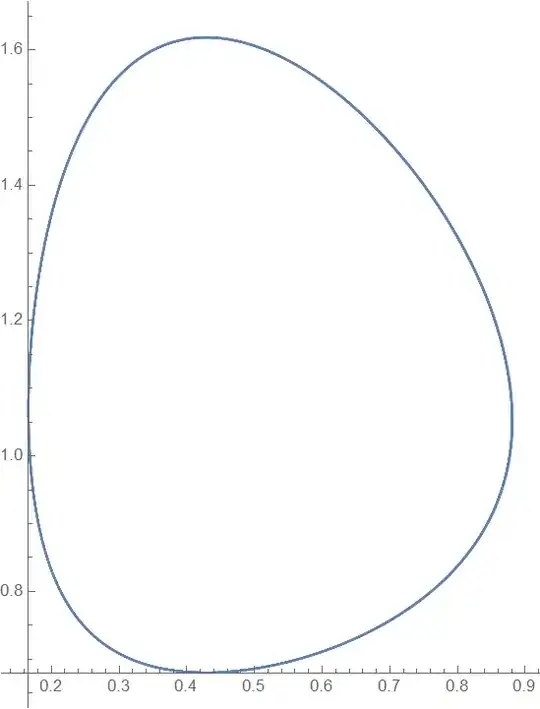
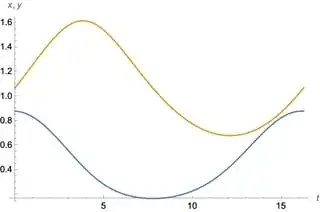
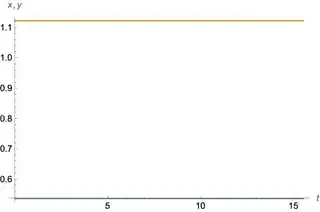
enter image description here

Hope it helps!

Ulrich Neumann
  • 53,729
  • 2
  • 23
  • 55
  • I would not have thought of approaching it this way. Thanks. My test is therefore gz[[1]] < Tol && 1 < (tp /. gz[[2]]) < MaxWin, where Tol is my desired tolerated distance between the start and end of an orbit and MaxWin is the longest suspected period. – user12734 Jun 16 '23 at 15:39
1

A few initial thoughts:

  1. Since limit cycles are defined for $t\to\infty$, you'll never be quite sure with finite time. This will be especially problematic near a bifurcation point, where transients last longer.
  2. You can simplify (x[t] - 1) / (x[t]^2 - 1) to 1 / (x[t] + 1).
  3. With that simplification, this becomes the well-known Rosenzweig-MacArthur predator-prey model.

With those points out of the way, I can suggest that this will be easier if if you're willing to use my EcoEvo package. First, install it with:

PacletInstall["EcoEvo", "Site" -> "http://raw.githubusercontent.com/cklausme/EcoEvo/master"]

Now load the package and set the model for analysis:

<< EcoEvo`

SetModel[{
  Aux[x] -> {Equation :> x - 0.5 x^2 - x y /(x + 1)},
  Aux[y] -> {Equation :> -m y + x y/(x + 1)},
  Parameters -> {m}
}]

Then you can find a limit cycle with FindEcoLimitCycle, and check its final derivatives to make sure it's not an equilibrium.

A limit cycle:

m = 0.3;
PlotEcoPhasePlane[{x, 0, 2}, {y, 0, 2}]
ec = FindEcoCycle[{x -> 0.1, y -> 0.1}];
PlotDynamics[ec]
FinalDerivatives[ec]

enter image description here enter image description here

(* {x' -> -0.00828357, y' -> 0.179955} *)

An equilibrium:

m = 0.35;
PlotEcoPhasePlane[{x, 0, 2}, {y, 0, 2}]
ec = FindEcoCycle[{x -> 0.1, y -> 0.1}];
PlotDynamics[ec]
FinalDerivatives[ec]

enter image description here enter image description here

(* {x' -> -4.6931*10^-7, y' -> 2.49523*10^-7} *)

I'm working on some new functionality to track limit cycles vs a parameter, but that's not quite ready.

Chris K
  • 20,207
  • 3
  • 39
  • 74
0

First try to find the steady solution

dgl[m_] := {x'[t] ==x[t] - 1/2 x[t]^2 - x[t] y[t] (x[t] - 1)/(x[t]^2 - 1),y'[t] == -m y[t] + x[t] y[t] (x[t] - 1)/(x[t]^2 - 1) }

T = 500;


m = 0.35;
{X, Y} = NDSolveValue[{dgl[m], x[0] == 0.1, y[0] == 0.1 }, {x, y}, {t, 0, T}];
{X, Y} = NDSolveValue[{dgl[m], x[0] == X[T], y[0] == Y[T] }, {x, y}, {t, 0, T}];  (* steady solution*)

equilibrium

equi =  First@Solve[{0 == x[t] - 1/2 x[t]^2 - x[t] y[t] (x[t] - 1)/(x[t]^2 - 1),0 == -m y[t] + x[t] y[t] (x[t] - 1)/(x[t]^2 - 1) }, {x[t], y[t]}] /. f_[t] -> f; 
{x\[Infinity], y\[Infinity]} = {{x /. equi}, {y /. equi}}
(*{{0.538462}, {1.12426}}*)

Plot[ Norm[ {X[t] - x[Infinity], Y[t] - y[Infinity]} ]  , {t, 0, T},PlotLabel->"m="<>ToString[m]]

enter image description here

Result m==.3

m = 0.3 ;
{X, Y} = NDSolveValue[{dgl[m], x[0] == 0.1, y[0] == 0.1 }, {x, y}, {t, 0,T}];
{X, Y} = NDSolveValue[{dgl[m], x[0] == X[T], y[0] == Y[T] }, {x, y}, {t, 0,T}];  (* steady solution*)
equi =  First@
Solve[{0 == x[t] - 1/2 x[t]^2 - x[t] y[t] (x[t] - 1)/(x[t]^2 - 1),0 == -m y[t] + x[t] y[t] (x[t] - 1)/(x[t]^2 - 1) }, {x[t], y[t]}] /. f_[t] -> f; 
{x\[Infinity], y\[Infinity]} = {{x /. equi}, {y /. equi}}
(*{{0.428571}, {1.12245}}*)
Plot[ Norm[ {X[t] - x\[Infinity], Y[t] - y\[Infinity]} ]  , {t, 0,T},PlotLabel->"m="<>ToString[m]]

enter image description here

Ulrich Neumann
  • 53,729
  • 2
  • 23
  • 55
  • If I'm interpreting this correctly, then the second use of NDSolveValue[] simply picks up from where the first use ends. Why is this different from implementing it once for `{t,0,2 T}'? My interpretation of the rest that it's simply subtracting the steady state. Thus I don't see how it contributes to detecting an orbit. – user12734 Jun 16 '23 at 15:36
  • @user12734 Both cases show a periodic orbid. Plot of the norm shows a finite orbit or a vanishing orbit. – Ulrich Neumann Jun 16 '23 at 19:17
0

Although the suggestion made by Ulrich Neumann works for detecting orbits in general, it is not robust to "vanishing orbits", i.e. damped oscillations, as his subsequent suggestion points out. (My interest is in the detection of stable limit cycles only.)

Finite-time challenges aside, I tried some variations on his method of estimating the period (incl. allowing for multiple tp solutions and using FFT). However, in the end, modifying my originally-posted method (increasing T, testing for convergence to a fixed point using a lagged time comparison, increasing Accuracy and Precision goals) proved to get me closest to what I desire.

test2[m_] :=
 Module[{X, Y, res, T, Tlag, Diff, Tol},
  T = 150000;
  Tlag = 100;
  Tol = 10^-5;

{X, Y} = 
   NDSolveValue[{sys[m], x[0] == 0.1, y[0] == 0.1}, {x, y}, {t, 0, 
     T}, AccuracyGoal -> 10, PrecisionGoal -> 10];


Diff = Abs[X[T] - X[T - Tlag]];
  If[Diff < Tol,
   res = {1},
   res = 
    Reap[nd[{m}] = NDSolve[{{sys[m], x[0] == X[T], y[0] == Y[T]},
         WhenEvent[x'[t] == 0, Sow[{m, Round[y[t], Tol]}]]}, {x[t], 
         y[t]}, {t, 0, T}, AccuracyGoal -> 10, PrecisionGoal -> 10,
        MaxSteps -> [Infinity]]][[-1, 1]]
   ];
  CountDistinct[res] == 2
  ]
user12734
  • 349
  • 1
  • 7