These are the equations of the dynamical system
Vn = (-G*Mn)/Sqrt[x[t]^2 + y[t]^2 + cn^2];
Vd = (-G*Md)/Sqrt[x[t]^2 + y[t]^2 + (s + h)^2];
Vh = (-G*Mh)/Sqrt[x[t]^2 + y[t]^2 + ch^2];
Vb = (G*Mb)/(2*a)*(ArcSinh[(x[t] - a)*(y[t]^2 + c^2)^(-1/2)] -
ArcSinh[(x[t] + a)*(y[t]^2 + c^2)^(-1/2)]);
pot = Vn + Vd + Vh + Vb;
H = 1/2*(ux[t]^2 + uy[t]^2) + pot - om*(x[t]*uy[t] - y[t]*ux[t]);
and these are the values of the parameters
G = 1; Mn = 400; cn = 0.25;
Md = 7000; s = 3; h = 0.175;
Mb = 3500; a = 10; c = 1;
Mh = 20000; ch = 20;
om = 4.5;
H0 = -3180;
The initial conditions of the orbit are
x00 = 10.77; y0 = 0; ux0 = 0;
Ht = H /. {x[t] -> x00, y[t] -> y0, ux[t] -> ux0};
pot0 = pot /. {x[t] -> x00, y[t] -> y0};
py0 = x00*om - Sqrt[x00^2*om^2 + 2*(H0 - pot0)];
sol = Solve[Ht == H0];
uy0 = uy[t] /. sol[[1]]
tmin = 0; tmax = 1;
The set of the equations of motion
DifferentialEquations[H_, om_, x00_, y0_, ux0_, uy0_] :=
Module[{Deq1, Deq2, Deq3, Deq4},
Deq1 = x'[t] == ux[t] + om*y[t];
Deq2 = y'[t] == uy[t] - om*x[t];
Deq3 = ux'[t] == -D[pot, x[t]] + om*uy[t];
Deq4 = uy'[t] == -D[pot, y[t]] - om*ux[t];
{Deq1, Deq2, Deq3, Deq4, x[0] == x00, y[0] == y0, ux[0] == ux0,
uy[0] == uy0}
]
and the numerical integration
DE = DifferentialEquations[H, om, x00, y0, ux0, uy0];
sol = NDSolve[DE, {x[t], y[t], ux[t], uy[t]}, {t, tmin, tmax},
MaxSteps -> Infinity, Method -> "Adams",
PrecisionGoal -> 12, AccuracyGoal -> 12];
xx[t_] = x[t] /. sol[[1]];
yy[t_] = y[t] /. sol[[1]];
uxx[t_] = ux[t] /. sol[[1]];
uyy[t_] = uy[t] /. sol[[1]];
For x00 = 10.77 the corresponding orbit is the follwoing
plot = ParametricPlot[{xx[t], yy[t]}, {t, tmin, tmax}, Axes -> False,
Frame -> True, AspectRatio -> 1, PlotStyle -> Black,
AspectRatio -> 1, PlotRange -> All]
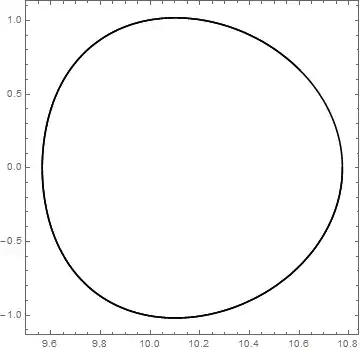
We see that the orbit is not periodic. However if we use x00 = 10.77403 we get
which is indeed a periodic orbit.
My question is obviously the following: how can I locate the exact (let's say with 10 decimal digits) position of the periodic orbit? Somehow inside the NDSolve there should be an iterative process changing the value of x00 until it hits the periodic point.
The corresponding FORTRAN code indicates that the position of the periodic orbit is at x00 = 10.774029735833850. So any provided method here must give the same result.
NOTE: The energy level H0 = -3180 should be remain the same while searching for the x00 value of the periodic orbit. x00 is always in the interval [9,12], so the initial guess 10.77 should be corrected somehow so as to hit the exact the periodic point. Also for x = x00 it should be y0 = ux0 = 0.
EDIT
DO loop for variable value of the energy
data = {};
Do[
x00 = 10.5; y0 = 0; ux0 = 0;
tmin = 0; tmax = 1;
Ht = H /. {x[t] -> x00, y[t] -> y0, ux[t] -> ux0};
pot0 = pot /. {x[t] -> x00, y[t] -> y0};
py0 = x00*om - Sqrt[x00^2*om^2 + 2*(H0 - pot0)];
sol = Solve[Ht == H0];
uy0 = uy[t] /. sol[[1]];
Clear[uy0];
fuy0[x0_] :=
Solve[(H /. {x[t] -> x0, y[t] -> y0, ux[t] -> ux0, uy[t] -> uy0}) ==
H0, uy0][[1, 1, 2]]
f[xp_, tp_] :=
Module[{xx = x[xp, fuy0[xp]] /. solp, yy = y[xp, fuy0[xp]] /. solp,
uxx = ux[xp, fuy0[xp]] /. solp,
uyy = uy[xp, fuy0[xp]] /.
solp}, {Norm[{xx[tp], yy[tp], uxx[tp], uyy[tp]} - {xx[0],
yy[0], uxx[0], uyy[0]}], Norm[xx[tp] - xx[0]]}]
DE = DifferentialEquations[H, om, x0, y0, ux0, uy0];
solp = ParametricNDSolve[
DE, {x, y, ux, uy}, {t, tmin, tmax}, {x0, uy0},
MaxSteps -> Infinity, Method -> "Adams", PrecisionGoal -> 12,
AccuracyGoal -> 12];
pos = Quiet@
FindRoot[f[xp, tp], {{xp, x00}, {tp, .5}}, PrecisionGoal -> 12,
AccuracyGoal -> 12];
xper = xp /. pos[[1]];
tper = tp /. pos[[2]];
AppendTo[data, {xper, tper}],
{H0, -3180, -3170, 1}
]


{x0, y0, ux0, uy0}free parms? – Dr. belisarius Oct 06 '15 at 13:03x00 = 10.77403(only five decimal digits) the orbit is periodic. – Vaggelis_Z Oct 06 '15 at 13:26