I'd call this a bug. I've seen cases where the letter makes difference in result (internally some code seems to use lexicographic ordering in some places? and this have this side effect of changing the expression form which affects some code). So this is not really new in Mathematica. It does not have to be special character for this to happen. I've put some related links at bottom
Here is a simpler example than your's showing this, also using Rubi to compare
Mathematica 13.3
ClearAll["Global`*"]
integrand1=z/Sqrt[-(r*(r-2*z))]
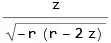
anti1=Integrate[integrand1,r]
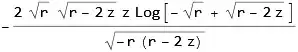
ReImPlot[anti1/.z->2,{r,-Pi,Pi},PlotRange->All]

Now simply change z to q in the integrand. Now the anti-derivative is completely different
integrand2=integrand1/.z->q

You see the integrand is same as before, just q instead of z
anti2=Integrate[integrand2,r]

ReImPlot[anti2/.q->2,{r,-Pi,Pi},PlotRange->All]

Rubi
Here changing the letter did not make difference as expected.
Quit[]
<<Rubi`
integrand1=z/Sqrt[-(r*(r-2*z))]
anti1=Int[integrand1,r]

ReImPlot[anti1/.z->2,{r,-Pi,Pi},PlotRange->All]

integrand2 = integrand1 /. z -> q
anti2 = Int[integrand2, r]

ReImPlot[anti2 /. q -> 2, {r, -Pi, Pi}, PlotRange -> All]

related links
Simplification depends on the names of variables
Why does simplification in Mathematica depend on variable names
Variable naming changes everything
Apart behaves differently depending on specific alphabetic letters of variables
DSolve—different solutions for same set of equations using different symbols?
Evaluating two equivalent integrals apparently gives two different results

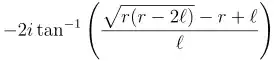
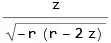
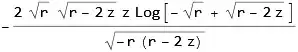








Undefinedunder the assumptions:Integrate[-((Sqrt[-r (r - 2 l)] l)/(r (r - 2 l) (-r + l))), {r, 0, r}, Assumptions -> {2 l > r > 0}]andIntegrate[-((Sqrt[-r (r - 2 l)] l)/(r (r - 2 l) (-r + l))) /. {l -> \[ScriptL]}, {r, 0, r}, Assumptions -> {2 \[ScriptL] > r > 0}]. This is seems a bug, whereas the different results in the indefinite integrals above I would call unsurprising and not a bug. – Michael E2 Jul 16 '23 at 14:25