How to combine Maximize with Asymptotic for $\operatorname{argmax}_t \frac{\sin (t) \sin ((n+1) t) \csc (n t)}{\pi }?$

Question

Can anyone see a trick to get large-$n$ formula for the maximum for the following for integer $n>0$ and $t\in \left( 0, \frac{\pi}{n+1}\right)$?

$$\frac{\sin (t) \sin ((n+1) t) \csc (n t)}{\pi }$$

Ideally I could use asymptotic + maximize, but that returns unevaluated

Asymptotic[
 Maximize[{(Csc[n t] Sin[t] Sin[(1 + n) t])/\[Pi], 
   0 < t < Pi/(n + 1)}, t], n -> \[Infinity]]

Plotting on log-log plot it appears to approach power law

getVal[n_] := 
  First@Maximize[{(Csc[n t] Sin[t] Sin[(1 + n) t])/\[Pi], 
      0 < t < Pi/(n + 1)}, t];
ListPlot[Table[getVal[n], {n, 1, 6}], 
 ScalingFunctions -> {"Log", "Log"}]

Background: this is weighted spectral density of a product of $n$ independent Gaussian matrices, ie getVal[1] is equivalent to Maximize[x PDF[MarchenkoPasturDistribution[1], x], x]

Answer 1

A typical case is as follows.

n = 26; Plot[(Csc[n t] Sin[t] Sin[(1 + n) t])/Pi, {t, 0, Pi/(n + 1)}]

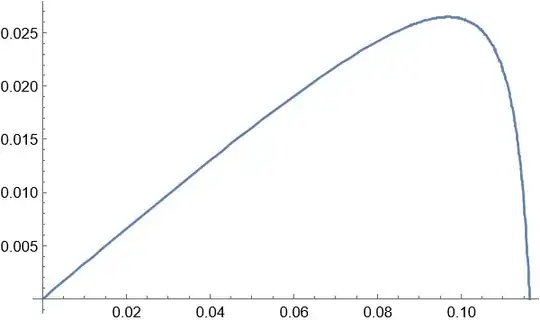
We see the maximum of the differentiable in $t$ function under consideration is reached near $t=\frac \pi {n+1}$. In view of it we substitute t -> Pi/(n + 1) - a in its derivative and expand the derivative by powers of a near zero.

ClearAll[n];Series[D[(Csc[n t] Sin[t] Sin[(1 + n) t])/Pi, t] /. 
t -> Pi/(n + 1) - a, {a, 0, 1}] // Normal

-(((1 + n) Csc[(n \[Pi])/(1 + n)] Sin[\[Pi]/( 1 + n)])/\[Pi]) - (1/\[Pi]) 2 a (-Cos[\[Pi]/(1 + n)] Csc[(n \[Pi])/(1 + n)] - n Cos[\[Pi]/(1 + n)] Csc[(n \[Pi])/(1 + n)] + n Cot[(n \[Pi])/(1 + n)] Csc[(n \[Pi])/(1 + n)] Sin[\[Pi]/( 1 + n)] + n^2 Cot[(n \[Pi])/(1 + n)] Csc[(n \[Pi])/(1 + n)] Sin[\[Pi]/( 1 + n)])

({a, 0, 2} does not make things better.) Then we equate the above to zero and solve in a.

sol=Solve[% == 0, a]

{{a -> Sin[\[Pi]/(1 + n)]/( 2 (Cos[\[Pi]/(1 + n)] - n Cot[(n \[Pi])/(1 + n)] Sin[\[Pi]/(1 + n)]))}}

We are interested in the maximum value so we substitute that value of a in the function.

((Csc[n t] Sin[t] Sin[(1 + n) t])/Pi /. t -> Pi/(n + 1) - a) /. sol

{(1/\[Pi]) Csc[n (\[Pi]/(1 + n) - Sin[\[Pi]/(1 + n)]/( 2 (Cos[\[Pi]/(1 + n)] - n Cot[(n \[Pi])/(1 + n)] Sin[\[Pi]/(1 + n)])))] Sin[\[Pi]/( 1 + n) - Sin[\[Pi]/(1 + n)]/( 2 (Cos[\[Pi]/(1 + n)] - n Cot[(n \[Pi])/(1 + n)] Sin[\[Pi]/(1 + n)]))] Sin[(1 + n) (\[Pi]/(1 + n) - Sin[\[Pi]/(1 + n)]/( 2 (Cos[\[Pi]/(1 + n)] - n Cot[(n \[Pi])/(1 + n)] Sin[\[Pi]/(1 + n)])))]}

At last, in order to find the asymptotic,

Series[%, {n, Infinity, 2}]

{1/(3 n)-7/(18 n^2)+O[1/n]^3}

Calculations confirm the exponent -1.

getVal[n_] := First@NMaximize[{(Csc[n t] Sin[t] Sin[(1 + n) t])/\[Pi],
 0 < t < Pi/(n + 1)}, t];Table[Log[getVal[n]]/Log[n], {n, 200, 260}]

{-1.02648, -1.02639, ... , -1.02222, -1.02217}

Addition. Here is my successful attempt. Let us write down $\sin((n+1)t)=\sin(nt)\cos(t)+\cos(nt)\sin(t)$. Because $t\in \left[0,\frac \pi {n+1}\right]$ and $n$ tends to $\infty$, I replace $\sin(t)$ by $t$ and $\cos(t)$ by $1- \frac {t^2} 2$. It's summer now and I'm not in the mood to give error estimates. Let us look at a typical case

n = 26; Plot[{(Sin[n*t]*(1 - t^2/2) + Cos[n*t]*t)*t*Csc[n*t]/Pi, 
(Sin[t]* Csc[n t] Sin[(1 + n) t])/\[Pi]}, {t, 0, Pi/n}, PlotStyle -> {Red, {Blue, Dashed}}]

It is convenient to make a replacement

ClearAll[n]; (Sin[n*t]*(1 - t^2/2) + Cos[n*t]*t)*t*Csc[n*t]/Pi /. t -> x/n

(x Csc[x] ((x Cos[x])/n + (1 - x^2/(2 n^2)) Sin[x]))/(n \[Pi])

Now we expand it around Pi

b = Series[(x Csc[x] ((x Cos[x])/n + (1 - x^2/(2 n^2)) Sin[x]))/(n*Pi), {x, Pi, 4}] // Normal

(4 n + 2 n^2 - \[Pi]^2)/(2 n^3) + \[Pi]/( n^2 (-\[Pi] + x)) + ((6 n + 6 n^2 - 9 \[Pi]^2 - 2 n \[Pi]^2) (-\[Pi] + x))/( 6 n^3 \[Pi]) + ((-9 - 4 n) (-\[Pi] + x)^2)/( 6 n^3) + ((-45 - 30 n - 2 n \[Pi]^2) (-\[Pi] + x)^3)/( 90 n^3 \[Pi]) - (2 (-\[Pi] + x)^4)/(45 n^2)

I repeat it's summer now and I'm not in the mood to give error estimates.

Maximize[{b, x >= Pi/2 && x <= Pi && n >= 35}, x] // First

produces a huge result in terms of a Root of a polynomial of 5-th degree. Now

Series[%, {n, Infinity, 1}]

1/n+O[1/n]^(3/2)

Calculations confirm it by

getVal[n_] := First@NMaximize[{(Csc[n t] Sin[t] Sin[(1 + n) t])/\[Pi], 
0 < t < Pi/(n + 1)}, t]; Table[getVal[n]*n, {n, 3000000, 3000020}]

{0.998846, 0.998846, 0.998846, 0.998846, 0.998846, 0.998846, 0.998846, 0.998846, 0.998846, 0.998846, 0.998846, 0.998846, 0.998846, 0.998846, 0.998846, 0.998846, 0.998846, 0.998846, 0.998846, 0.998846, 0.998846}

Moreover, the result of

getVal[n_] := First@NMaximize[{(Csc[n t] Sin[t] Sin[(1 + n) t])/\[Pi],  0 < t < Pi/(n + 1)}, t]; 
Table[(getVal[n] - 1/n)*n^(3/2), {n, 3000000, 5000000, 500000}]

{-1.99884, -1.99893, -1.99902, -1.99906, -1.99911}

confirms $O(n^{-3/2}),\,n\to \infty.$