0

How do I use NetChain to obtain a fit that is at least accurate on the training data?

I am trying to get a hopefully predictive fit for some data (see my question Fitting smooth monotonic function (low number of points, irregular grid)). But in the process I found I was already getting stumped on something much more elementary. I couldn't even managed to get a (possibly over-fitted) fit that actually goes close to the points in the training data.

What do I need to do adjust to obtain a fit that is at least accurate on the training data? (Should I add more layers, change the training termination criteria...?)

data={{3.38, 1.028877662, 2.009398505, 2.067322478, 4.214191194}, {3.4, 
  1.030082372, 1.995543604, 2.105894366, 4.234656059}, {3.5, 
  1.035994874, 1.992385102, 2.200815333, 4.282937808}, {3.57, 
  1.036731784, 1.986961442, 2.224357922, 4.307824219}, {3.6, 
  1.036978228, 1.985081926, 2.231988058, 4.315914728}, {3.62, 
  1.037229736, 1.983076125, 2.239730469, 4.323988127}, {3.78, 
  1.038461995, 1.969909372, 2.283628754, 4.374960036}, {3.8, 
  1.038741973, 1.96716995, 2.291334094, 4.384253554}}

Example try (I tried different things with more or less layers or different activation functions too):

net = NetChain[{30, Tanh, 30, Tanh, 30, Tanh, 30, Tanh, 30, 1}, "Input" -> "Scalar", 
  "Output" -> "Scalar"]
trainingSet = (#1 -> #3 & @@@ data);
NetInitialize[net];
net = NetTrain[net, trainingSet];

Example fit:

enter image description here

I would like to have a fit that deviates from the data in the training set at most by say 10^-15. (The data is exact up to 30 digits and so I would like a fit to reproduce it to high accuracy.)

P.S. The data as posted here is obviously only accurate to at most 9 digits but that is just the truncation I used here to keep the post readable. I don't think the error introduced by this rounding will pose any problem to finding a fit but if for some method it does I can provide the high precision data.

Kvothe
  • 4,419
  • 9
  • 28
  • 1
    Why are you using neural networks for fitting 7 points? @BobHanlon showed you in his answer how to do a polynomial fit. Also note that there are infinitely many possible functions which go through these 7 points. Getting an "accurate" fit depends on what this data actually represent and what the underlying function is supposed to be. – Domen Jul 31 '23 at 17:03
  • Right, might not be the right tool. Still it puzzles me that I can't even get it to (over)fit. Hence this question. – Kvothe Jul 31 '23 at 17:36
  • Rest of my reply is more related to the question you reference. Sure there are infinitely many functions but perhaps I wasn't clear in the other question but I still expect something like occam's razor to hold. The parts of these functions seem pretty well approximated by linear and cubic polynomials as long as I split the function up. As a whole it clearly needs a much higher order polynomial. Note that BobHanlon's suggested fit is absolutely terrible FindFormula is just using linear fits which clearly don't fit at all. (O it was, just updated so I will have to check again.) – Kvothe Jul 31 '23 at 17:37
  • I can obtain decent fits by putting a lot of effort by hand (looking what the pattern is going from a part where the function is linear to cubic or fine tuning orders of polynomials) but the whole point is to automate this process. (Yes I do not define mathematically what makes a fit good. If you want perhaps good criteria for that question would be as smooth as possible while being monotonic and going through the provided data points.

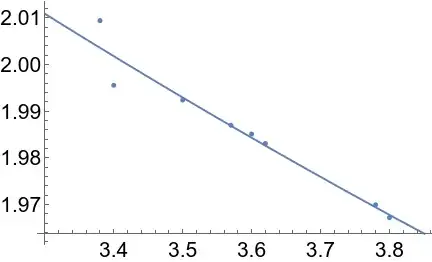
    (Polynomial fits can be ok when fine tuning the order (~7 in this case) but they have a tendency to break monotonicity.)

     – Kvothe Jul 31 '23 at 17:41
  • Any suggestion (probably best made on the linked question) for a different method I should try are of course welcome. So far I have been playing with polynomial fits, constrained spline fits maximizing smoothness, and imposing monotonicity on a discrete set of points. So far the best was just a polynomial fit fine tuning the order but I want to automate that work. And polynomial fits tend not to be monotonic as this data is. – Kvothe Jul 31 '23 at 17:48
  • @DanielHuber, what did you run exactly? NonlinearModelFit[data[[All,{1,3}]], {a1 } Exp[-a2 (x - a3)^2], {a1, a2, a3}, x] which I think is what you meant returns the warning "Failed to converge to the requested accuracy or precision within 100 iterations" and gives a terrible fit. Did you mean that? – Kvothe Aug 01 '23 at 12:33
  • (Also edited the plot to include all data points since as Daniel pointed out it was a bit deceiving before.) – Kvothe Aug 01 '23 at 12:38
  • Your NetChain fits the training data much better if you normalize the inputs.

    For example:

    net = NetChain[{BatchNormalizationLayer[], 30, Tanh, 30, Tanh, 30, Tanh, 30, Tanh, 30, 1}, "Input" -> "Scalar", "Output" -> "Scalar"];

    Then, NetTrain with a low LearningRate so the net converges to an optimum. https://i.imgur.com/6zstnE8.png

     – Dropped Bass Aug 30 '23 at 03:30

0 Answers0