Analyzing football games (pairing matrix)

Question

I want to cross-tabulate football games over several years.

Setting up example pairings:

Please note that there can be up to 20 clubs and a couple of thousand matches!

teams = {"Arsenal", "Brighton", "Chelsea"};
n = 30; (* number of matches *)
SeedRandom[0];
games = RandomChoice[Permutations[teams, {2}], n]

{{"Chelsea", "Brighton"}, {"Arsenal", "Chelsea"}, {"Arsenal", "Brighton"}, {"Chelsea", "Arsenal"}, {"Arsenal", "Brighton"}, {"Chelsea", "Arsenal"}, {"Arsenal", "Chelsea"}, {"Brighton", "Arsenal"}, {"Arsenal", "Chelsea"}, {"Arsenal", "Brighton"}, {"Brighton", "Chelsea"}, {"Brighton", "Chelsea"}, {"Chelsea", "Arsenal"}, {"Brighton", "Arsenal"}, {"Arsenal", "Brighton"}, {"Chelsea", "Arsenal"}, {"Arsenal", "Chelsea"}, {"Brighton", "Chelsea"}, {"Arsenal", "Brighton"}, {"Brighton", "Chelsea"}, {"Chelsea", "Arsenal"}, {"Arsenal", "Chelsea"}, {"Brighton", "Arsenal"}, {"Chelsea", "Brighton"}, {"Brighton", "Arsenal"}, {"Brighton", "Arsenal"}, {"Arsenal", "Chelsea"}, {"Brighton", "Arsenal"}, {"Brighton", "Chelsea"}, {"Arsenal", "Chelsea"}}

It should be noted that (unlike a yearly league) games per team might be different:

Chelsea has played 19 games (over several years),

Total @ Cases[{x : {_, _}, c_} /; MemberQ[x, "Chelsea"] :> c] @ Tally @ games

19

but Arsenal had 23 matches.

Awarding points:

SeedRandom[0];
points = RandomChoice[{3, 1, 0}, n];

{0, 0, 1, 3, 3, 0, 3, 3, 0, 3, 1, 1, 1, 0, 3, 3, 3, 1, 0, 1, 0, 0, 3, 0, 3, 1, 3, 3, 0, 1}

games = Transpose[{games, points}];

If there is a draw both teams must get 1 point:

draws = games /. {{a_String, b_}, 1} :> Splice[{{{a, b}, 1}, {{b, a}, 1}}];

For a lost game the other team must get three points:

data = draws /. {{a_String, b_}, 0} :> Splice[{{{a, b}, 0}, {{b, a}, 3}}] // Sort

{{{"Arsenal", "Brighton"}, 0}, {{"Arsenal", "Brighton"}, 1}, {{"Arsenal", "Brighton"}, 1}, {{"Arsenal", "Brighton"}, 3}, {{"Arsenal", "Brighton"}, 3}, {{"Arsenal", "Brighton"}, 3}, {{"Arsenal", "Brighton"}, 3}, {{"Arsenal", "Chelsea"}, 0}, {{"Arsenal", "Chelsea"}, 0}, {{"Arsenal", "Chelsea"}, 0}, {{"Arsenal", "Chelsea"}, 1}, {{"Arsenal", "Chelsea"}, 1}, {{"Arsenal", "Chelsea"}, 3}, {{"Arsenal", "Chelsea"}, 3}, {{"Arsenal", "Chelsea"}, 3}, {{"Arsenal", "Chelsea"}, 3}, {{"Arsenal", "Chelsea"}, 3}, {{"Brighton", "Arsenal"}, 0}, {{"Brighton", "Arsenal"}, 1}, {{"Brighton", "Arsenal"}, 1}, {{"Brighton", "Arsenal"}, 3}, {{"Brighton", "Arsenal"}, 3}, {{"Brighton", "Arsenal"}, 3}, {{"Brighton", "Arsenal"}, 3}, {{"Brighton", "Arsenal"}, 3}, {{"Brighton", "Chelsea"}, 0}, {{"Brighton", "Chelsea"}, 1}, {{"Brighton", "Chelsea"}, 1}, {{"Brighton", "Chelsea"}, 1}, {{"Brighton", "Chelsea"}, 1}, {{"Brighton", "Chelsea"}, 3}, {{"Brighton", "Chelsea"}, 3}, {{"Chelsea", "Arsenal"}, 0}, {{"Chelsea", "Arsenal"}, 0}, {{"Chelsea", "Arsenal"}, 1}, {{"Chelsea", "Arsenal"}, 1}, {{"Chelsea", "Arsenal"}, 3}, {{"Chelsea", "Arsenal"}, 3}, {{"Chelsea", "Arsenal"}, 3}, {{"Chelsea", "Arsenal"}, 3}, {{"Chelsea", "Arsenal"}, 3}, {{"Chelsea", "Brighton"}, 0}, {{"Chelsea", "Brighton"}, 0}, {{"Chelsea", "Brighton"}, 1}, {{"Chelsea", "Brighton"}, 1}, {{"Chelsea", "Brighton"}, 1}, {{"Chelsea", "Brighton"}, 1}, {{"Chelsea", "Brighton"}, 3}}

Expected result:

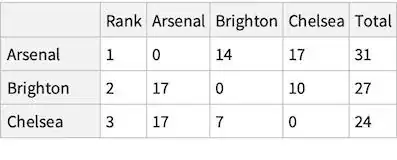
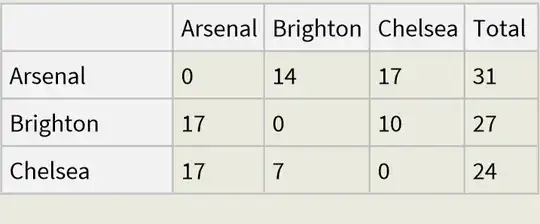
This is as far as I got, but I couldn't find a presentable way to build a pairing matrix. Doing it manually counting the above points gives:

result =
  <|"Arsenal" -> <|"Rank" -> 1, "Arsenal" -> 0, "Brighton" -> 14, "Chelsea" -> 17, "Total" -> 31|>, 
   "Brighton" -> <|"Rank" -> 2, "Arsenal" -> 17, "Brighton" -> 0, "Chelsea" -> 10, "Total" -> 27|>, 
   "Chelsea" -> <|"Rank" -> 3, "Arsenal" -> 17, "Brighton" -> 7, "Chelsea" -> 0, "Total" -> 24|>|>;
result // Dataset

The result doesn't need to be a Dataset - I welcome any matrix-like solution.

Must be a mid-season result: Arsenal are top of the league – user1066 Sep 11 '23 at 08:30 — user1066, Sep 11 '23 at 08:30
Well, that's an old problem of all random generators – eldo Sep 11 '23 at 08:33 — eldo, Sep 11 '23 at 08:33

score 7 · Answer 1 · answered Sep 10 '23 at 13:51

One way to do it:

aggResults = GroupBy[data, First -> Last, Total]

<|{"Arsenal", "Brighton"} -> 14, {"Arsenal", "Chelsea"} -> 17, {"Brighton", "Arsenal"} -> 17, {"Brighton", "Chelsea"} -> 10, {"Chelsea", "Arsenal"} -> 17, {"Chelsea", "Brighton"} -> 7|>

teamKeys = MapThread[Rule, {#, Range[Length@#]}] &[Union@Flatten@Keys@aggResults]

{"Arsenal" -> 1, "Brighton" -> 2, "Chelsea" -> 3}

results = SparseArray[(#[[1]] /. teamKeys) -> #[[2]] & /@ Normal@aggResults] // Normal

{{0, 14, 17}, {17, 0, 10}, {17, 7, 0}}

totals = Total /@ results

{31, 27, 24}

ranking = # /. Thread[Reverse@Sort@# -> Range[Length@#]] &@totals

{1, 2, 3}

header = (First /@ SortBy[teamKeys, Last])~Join~{"Totals", "Ranking"}

{"Arsenal", "Brighton", "Chelsea", "Totals", "Ranking"}

matrix =  Transpose[{{""}~Join~(First /@ SortBy[teamKeys, Last])}~Join~Transpose[{header}~Join ~Transpose[Transpose@results~Join~{totals, ranking}]]]
matrix // TableForm
(*Output*)

score 7 · Accepted Answer · answered Sep 10 '23 at 16:38

You can use GroupBy, Query (with the "add a column" syntax, and ReverseSortBy.

With OP initial values of teams, n, games, and points,

gamepoints = Transpose[{games, points}] /. {
   {{a_, b_}, 0} :> {{b, a}, 3}
   , g : {{a_, b_}, 1} :> Sequence[g, {{b, a}, 1}]
   };

and

Dataset[
 pairmx =
  ReverseSortBy[#["Total"] &]@
   Query[
     All
     , <|KeySort[#], "Total" -> Total@#|> &
     ]@
    GroupBy[
     Join[gamepoints, {{#, #}, 0} & /@ teams]
     , {First@*First, Last@*First -> Last}
     , Total
     ]
 ]

Rank is same as position index. Query or Part will do.

Query[2, "Chelsea"]@pairmx

and

pairmx[[2, "Chelsea"]]

both give

Also by name

Query["Brighton", "Chelsea"]@pairmx

and

pairmx[["Brighton", "Chelsea"]]>

both give

Hope this helps.

Daniel Huber · Answer 3 · 2023-09-10T15:02:09.667

Starting from your "data", we scan every element and use "Sow" to put the points in a list. "Sow" works like "first com, first served". Therefore, to get the pts in the correct order, we make some dummy entries using "Nothing".

Having the points in order, we may add them up and partition them according to the club. Then we sort the points according to the total. Finally we add the rank.

"pts" can now be displayed using "TableForm":

pts = Reap[Do[Sow[Nothing[], i], {i, 12}];
   Scan[Switch[#,
      {{"Arsenal", _}, _}, Sow[#[[2]], 4]; Sow[0, 1];
      Which[
       #[[1, 2]] == "Brighton", Sow[#[[2]], 2],
       #[[1, 2]] == "Chelsea", Sow[#[[2]], 3]],
      {{"Brighton", _}, _}, Sow[#[[2]], 8]; Sow[0, 6];
      Which[
       #[[1, 2]] == "Arsenal", Sow[#[[2]], 5],
       #[[1, 2]] == "Chelsea", Sow[#[[2]], 7]],
      {{"Chelsea", _}, _}, Sow[#[[2]], 12]; Sow[0, 11];
      Which[
       #[[1, 2]] == "Arsenal", Sow[#[[2]], 9],
       #[[1, 2]] == "Brighton", Sow[#[[2]], 10]]
      ] &
    , data]
   ][[2]];
pts = Partition[Total /@ pts, 4];
SortBy[pts, (-1 Last[#]) &];
pts = Transpose[Prepend[Transpose@pts, Range[Length[pts]]]];
TableForm[pts, 
 TableHeadings -> {{"Arsenal", "Brighton", "Chelsea"}, {"Rank", 
    "Arsenal", "Brighton", "Chelsea", "Total"}}]

Addendum

Here is a version than can del with any number of teams:

teams= DeleteDuplicates[data[[All, 1, 1]]];
getpts[{{win_, loos_}, pt_}] := 
  Module[{posw = Position[teams, win][[1, 1]], 
    posl = Position[teams, loos][[1, 1]]},
   Sow[pt, 4 posw];
   Sow[pt, 4 (posw - 1) + posl];
   Sow[0, 4 (posw - 1) + posw];
   ];
pts = Reap[Do[Sow[Nothing[], i], {i, 12}];
    Scan[
     Do[Sow[Nothing[], i], {i, 4 Length[teams]}];
     getpts
     , data]
    ][[2]];
pts = Partition[Total /@ pts, 4];
SortBy[pts, (-1 Last[#]) &];
pts = Transpose[Prepend[Transpose@pts, Range[Length[pts]]]];
TableForm[pts, 
 TableHeadings -> {teams, Join[{"Rank"}, teams, {"Total"}]}]

Sorry, I should have added that there can be up to 20 teams - +1 anyway — eldo, Sep 10 '23 at 13:23
I have added a version that can deal with any number of teams — Daniel Huber, Sep 10 '23 at 15:02

score 4 · Answer 4 · answered Sep 10 '23 at 16:21

Assuming data is stored in a variable called data:

Block[{original = 
   Dataset @ GroupBy[Flatten /@ data, First -> Rest, 
     GroupBy[#, First -> Last, Total] &], transposed, keys},
(Automatically add Missing on Diagonal)
 transposed = GeneralUtilities`AssociationTranspose @ Normal @ original;
(Used for placing Total / Rank)
 keys = Normal @ Keys @ original;
(Use Dataset Query to calculate the Total)
 transposed["Total"] = 
  AssociationThread[keys -> Normal @ Values @ original[All, Total]];
(Use Dataset Query to Find Ordering)
 transposed["Rank"] = 
  AssociationThread[keys -> Normal @ original[Reverse @* Ordering, Total]];
Dataset @ GeneralUtilities`AssociationTranspose @ transposed
 ]

Output:

Very nice! - For better readability: Query[Transpose]@Normal@original — eldo, Sep 10 '23 at 16:34

score 2 · Answer 5 · answered Sep 10 '23 at 18:19

teams = {"Arsenal", "Brighton", "Chelsea"}; n = 30; 
SeedRandom[0]; games = RandomChoice[Permutations[teams, {2}], n]
SeedRandom[0]; points = RandomChoice[{3, 1, 0}, n]
games = Transpose[{games, points}]

games2 = Flatten[Table[Switch[g[[2]],
    0, {{Reverse[g[[1]]], 3}},
    1, {g, {Reverse[g[[1]]], 1}},
    3, {g}], {g, games}], 1]

totals = 
 Table[Total[Cases[games2, {{t, opp}, x_} -> x]], {t, teams}, {opp, teams}]

{{0, 14, 17}, {17, 0, 10}, {17, 7, 0}}

results = 
 ReverseSortBy[
  Table[Join[{teams[[n]]}, totals[[n]], {Total[totals[[n]]]}], {n, 
    Length[teams]}], Last]
TableForm[Table[Insert[results[[n]], n, 2], {n, Length[results]}], 
 TableHeadings -> {None, Flatten[Join[{"team", "rank"}, teams, {"total"}]]}]

Analyzing football games (pairing matrix)

5 Answers5

Output:

Linked