Can the Debye functions be implemented using built-in functions?

Question

It is claimed in the comments here that the Debye functions can be implemented using built-in special functions. This is clearly true for some Debye functions, e.g., $D_n^{(1)}(x)$ for $n = 1, 2, 3$ (see linked article, which gives these explicitly). However, I'm not sure whether the comment holds in general.

For example, I'm interested in the following integral:

$$D_{-1}^{(2)}(x) = \int_x^\infty \frac{dt}t \frac1{e^t - 1}.$$

Can this integral be represented exactly, in closed form, using built-in special functions? More generally, can the functions $D_n^{(1)}$ and $D_n^{(2)}$ be represented exactly for all integer $n$?

Edit: By "represented exactly, in closed form, using built-in special functions" I mean using built-in functions that are quickly evaluated numerically, without relying on NIntegrate or NSolve or other explicit numerical functions.

Answer 1

This only partially answers your question so I'll delete if it is not what you're looking for.

The first type of functions, $D^{(1)}_n (x)$ satisfy the differential equation $$D^{'(1)}_n (x) = \frac{x^n}{e^x-1} \\ \mathrm{with} \\ D^{(1)}_n (0) = 0$$

(I got the initial condition from looking at the integral definition on the MathWorld site at x = 0)

Edit: I missed on the MathWorld site it also mentions that $D^{(1)}_n (x)$ is only valid for $|x| < 2 \pi$, so just keep that in mind.

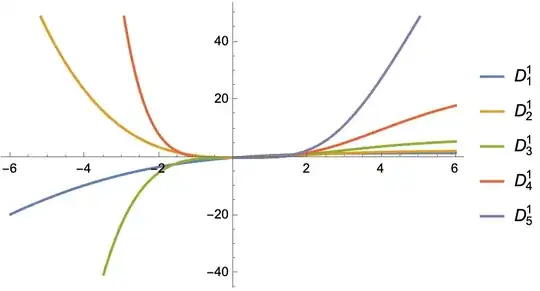
diff[n_] = D[d[x], x] == x^n/(E^x - 1);
soln1 = Table[ DSolveValue[{diff[n], d[0] == 0}, d[x], x], {n, 5}];
Plot[soln1, {x, -6, 6}, 
 PlotLegends -> Table[Subsuperscript[D, n, 1], {n, 5}]]

So we can write:

debyeD1[n_, x_] := DSolveValue[{diff[n], d[0] == 0}, d[x], x]

or alternatively using the integral definition:

debyeD1[n_, 
  x_] := (Integrate[x^n/(Exp[x] - 1), x] + (n! + Zeta[n + 1]))

The second type of functions, $D^{(2)}_n (x)$ satisfy the differential equation $$D^{'(2)}_n (x) = -\frac{x^n}{e^x-1} \\ \mathrm{with} \\ D^{(2)}_n (0) = n! \zeta (n+1)$$

This initial condition is also from the MathWorld site, as it says: $$D^{(1)}_n (x) + D^{(2)}_n (x) = n! \zeta (n+1)$$ And we know $D^{(1)}_n (0)$ is 0

diff2[n_] = D[d[x], x] == -(x^n/(E^x - 1));
soln2 = Table[ 
   DSolveValue[{diff2[n], d[0] == n! Zeta[n + 1]}, d[x], x], {n, 5}];
Plot[soln2, {x, -6, 6}, 
 PlotLegends -> Table[Subsuperscript[D, n, 2], {n, 5}]]

And confirming that the condition $$D^{(1)}_n (x) + D^{(2)}_n (x) = n! \zeta (n+1)$$ is met:

sums = soln1 + soln2;
sums/Table[n! Zeta[n + 1], {n, 5}] // Simplify
(*{1, 1, 1, 1, 1}*)

So we can write:

debyeD2[n_, x_] := 
 DSolveValue[{diff2[n], d[0] == n! Zeta[n + 1]}, d[x], x]

or alternatively using the integral definition:

debyeD2[n_, x_] := -Integrate[x^n/(Exp[x] - 1), x]

The only problem is I don't know how to do $D^{(2)}_{-1} (x)$

neg1 = {diff2[n], d[0] == n! Zeta[n + 1]}/.n->-1
(*{Derivative[1][d][x] == -(1/((-1 + E^x) x)), d[0] == ComplexInfinity}*)

because n! is not defined I believe at negative integers. Maybe someone else can fill in on this part. The integral definition doesn't evaluate either so I can't figure out how to show an exact form for $D^{(2)}_{-1} (x)$.