3D representation of a Boy surface using a mesh of tubes

Question

“Everything that matters in life flows through tubes.” - Georg Christoph Lichtenberg, The Waste Books

Model of a Boy surface at the Mathematical Research Institute of Oberwolfach, Germany

1. Preceding questions

This is (hopefully) the last of three questions concerning display options of ParametricPlot3D. The first two are

A perforated ding dong surface

and

Jeener's Flower

2. Parametrization

x = 1/2 * ((2 * a^2 - b^2 - c^2) + 2 * b * c * (b^2 - c^2) + c * a * (a^2 - c^2) + a * b * (b^2 - a^2));
y = 7/8 * ((b^2 - c^2) + c * a * (c^2 - a^2) + a * b * (b^2 - a^2));
z = -1/8 * (a + b + c) * ((a + b + c)^3 + 4 * (b - a) * (c - b) * (a - c));
boy = {x, y, z} /. {a :> Sin[u] * Sin[v], b :> Cos[u] * Sin[v], c :> Cos[v]};

3. ParametricPlot3D

The appearance of a Boy surface changes significantly with different viewpoints.

Table[
  ParametricPlot3D[boy, {u, 0, Pi}, {v, 0, Pi},
   Axes -> False,
   Boxed -> False,
   Lighting -> "ThreePoint",
   PlotPoints -> 40,
   PlotStyle -> MaterialShading["Iron"],
   ViewPoint -> v],
  {v, {Top, Below, {1.3, -2.4, 2}}}] // GraphicsRow

4. Tubification

To look inside and through the surface I tried:

ParametricPlot3D[boy, {u, 0, Pi}, {v, 0, Pi},
  Axes -> False,
  Mesh -> 12,
  PlotPoints -> 80,
  PlotStyle -> None,
  ViewPoint -> Above] /. Line :> ({Darker @ Red, Tube[#, 0.02]} &)

And to see the first two "generating" curves:

ParametricPlot3D[boy, {u, 0, Pi}, {v, 0, Pi},
  Axes -> False,
  Mesh -> 1,
  PlotPoints -> 40,
  PlotStyle -> None,
  ViewPoint -> Top] /. Line :> ({Darker @ Red, Tube[#, 0.02]} &)

5. Questions (sorted by relevance)

With my very basic appended tubification method I cannot colorize the tubes, nor can I apply a material to them.
The first tube plot has a very flat appearance. Maybe an appropriate lighting or another view angle would give a nicer result.
I would like to have an option to change the tube profile from round to rectangular.

Thank you in advance for your help and suggestions.

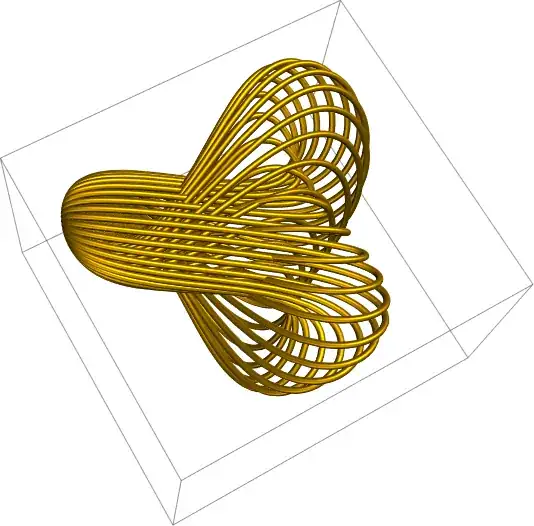
ParametricPlot3D[boy, {u, 0, Pi}, {v, 0, Pi}, Axes -> False, PlotPoints -> 100, Mesh -> 1, PlotStyle -> None, ViewPoint -> Above, MeshStyle -> {{MaterialShading[{"Glazed", Red}], Tube[0.07]}}]? — kglr, Oct 06 '23 at 11:43
Hi @eldo, these are great! If you're interested I have a parameterization for Girl's surface that I can share if you want to do that to. — Alex Mellnik, Oct 07 '23 at 15:07

kglr · Accepted Answer · 2023-10-07T04:18:11.717

Update: Using one-parameter ParametricPlot3D

{umesh, vmesh} = {Pi/2, Pi/2};
{boy1, boy2} = boy /. {{u -> umesh}, {v -> vmesh, u -> v}};
ParametricPlot3D[{boy1, boy2}, {v, 0, Pi}, 
  PlotStyle -> 
     {Tube[.1], 
      {MaterialShading["Iron"], Tube[.1]}}, 
  PlotPoints -> 50, 
  PlotRange -> All, 
  ColorFunction -> Hue, 
  Lighting -> "ThreePoint",
  ViewPoint -> Top, 
  Axes -> False]

ParametricPlot3D[Evaluate[Table[boy /. u -> i, {i, 0, Pi, Pi/30}]], 
 {v, 0, Pi}, 
 PlotStyle -> {{MaterialShading["Gold"], Tube[.02]}}, 
 PlotPoints -> 40, PlotRange -> All,  
 Lighting -> "ThreePoint", Axes -> False]

ParametricPlot3D[Evaluate[Table[boy /. v -> i, {i, 0, Pi, Pi/30}]], 
 {u, 0, Pi}, 
 PlotStyle -> Tube[.02],
 ColorFunction -> (Hue @ #4 &),
 PlotPoints -> 40, PlotRange -> All,  
 Lighting -> "ThreePoint", Axes -> False]

1. Colorize tubes and apply `MaterialShading`:

Post-processing

ParametricPlot3D[boy, 
   {u, 0, Pi}, {v, 0, Pi}, 
   Axes -> False, 
   Mesh -> 1, 
   PlotPoints -> 40, 
   PlotStyle -> None, 
   ViewPoint -> Top] /. 
 Line -> ({MaterialShading[{"Glazed", Red}], Tube[#, 0.07]} &)

Replace MaterialShading[{"Glazed", Red}] with MaterialShading["Iron"] to get

Use the rule

Line -> 
 ({Tube[#, 0.07, VertexColors -> (Hue /@ Subdivide[Length@#])]} &)

to get

MeshStyle with Tube as directive

Alternatively, you can use {directives, Tube[radius]} as a directive in MeshStyle:

ParametricPlot3D[boy, 
  {u, 0, Pi}, {v, 0, Pi},
  Axes -> False,  
  PlotPoints -> 100, 
  PlotStyle -> None, 
  ViewPoint -> Above,  
  Mesh -> 1, 
  MeshStyle -> {{MaterialShading[{"Glazed", Red}], Tube[0.07]}}]

Use MaterialShading["Iron"] to get

Use options ColorFunction -> Hue and MeshStyle -> {{Tube[0.07]}} to get

Is it possible to apply a ColorFunction and/or MaterialShading["Iron"]? — eldo, Oct 06 '23 at 13:14
@eldo, added some examples. I don't know how to apply ColorFunction and MaterialShading. — kglr, Oct 06 '23 at 13:40
I didn' want to use them together. The important thing is that I now can combine ColorFunction -> "AlpineColors" with MeshStyle -> Tube[0.02]. When was MeshStyle -> Tube[...] introduced? Couldn't find it in the docs. — eldo, Oct 06 '23 at 14:59
Tube[radius] as directive in PlotStyle or in MeshStyle is undocumented. I think I learned about it from this answer by John Fultz or/and from this answer by Yu-Sung Chang — kglr, Oct 06 '23 at 15:13

heropup · Answer 2 · 2023-10-07T01:59:20.290

Here is my code for the Bryant-Kunser parametrization of the Boy surface.

g[w_] := {-3/2 Im[w (1 - w^4)/(w^6 + Sqrt[5] w^3 - 1)],
          -3/2 Re[w (1 + w^4)/(w^6 + Sqrt[5] w^3 - 1)],
          Im[(1 + w^6)/(w^6 + Sqrt[5] w^3 - 1)] - 1/2};
b[u_, v_] := #/(#.#) &[g[v Exp[I u]]];

Interactive plot of the curves of constant $v$, with colored tubes:

Manipulate[ParametricPlot3D[b[u, v], {u, 0, 2 Pi}, 
     PlotRange -> {{-1.5, 1.5}, {-1.5, 1.5}, {-2, 1}},
     Boxed -> False, SphericalRegion -> True, Axes -> True,
     AxesOrigin -> {0, 0, 0},
     PlotStyle -> Directive[CapForm[None], JoinForm["Miter"]], 
     ColorFunction -> "AlpineColors", Method -> {"TubePoints" -> 30}] /. 
     Line[pts_, rest___] :> Tube[pts, 0.025, rest],
     {v, 0, 1}]

Interactive plot of the closed curves along $u$ and $u + \pi$:

Manipulate[ParametricPlot3D[{b[u, v], b[u + Pi, v]}, {v, 0, 1}, 
     PlotRange -> {{-1.5, 1.5}, {-1.5, 1.5}, {-2, 1}},
     Boxed -> False, SphericalRegion -> True, Axes -> True,
     AxesOrigin -> {0, 0, 0}, 
     PlotStyle -> Directive[CapForm[None], JoinForm["Miter"]], 
     ColorFunction -> "AlpineColors", Method -> {"TubePoints" -> 30}] /. 
     Line[pts_, rest___] :> Tube[pts, 0.025, rest],
     {u, 0, Pi}]

Combined plots:

ParametricPlot3D[Evaluate[Table[b[u, v], {v, 0, 1, .025}]], {u, 0, 2 Pi},
     PlotRange -> {{-1.5, 1.5}, {-1.5, 1.5}, {-2, 1}},
     Boxed -> False, SphericalRegion -> True, Axes -> True,
     AxesOrigin -> {0, 0, 0}, 
     PlotStyle -> Directive[CapForm[None], JoinForm["Miter"]], 
     ColorFunction -> "AlpineColors", Method -> {"TubePoints" -> 30}] /. 
     Line[pts_, rest___] :> Tube[pts, 0.025, rest]
ParametricPlot3D[Evaluate[Table[b[u, v], {u, Pi/40, 2 Pi, Pi/40}]], {v, 0, 1},
     PlotRange -> {{-1.5, 1.5}, {-1.5, 1.5}, {-2, 1}},
     Boxed -> False, SphericalRegion -> True, Axes -> True,
     AxesOrigin -> {0, 0, 0}, 
     PlotStyle -> Directive[CapForm[None], JoinForm["Miter"]], 
     ColorFunction -> "SunsetColors", Method -> {"TubePoints" -> 30}] /.
     Line[pts_, rest___] :> Tube[pts, 0.025, rest]

The code I've used has been adapted from the documentation of Tube, under Neat Examples; in particular, the options PlotStyle and Method for ParametricPlot3D, and the replacement of Line with Tube.

3D representation of a Boy surface using a mesh of tubes

2 Answers2

1. Colorize tubes and apply MaterialShading:

Post-processing

MeshStyle with Tube as directive

1. Colorize tubes and apply `MaterialShading`: