NDSolve producing oscillatory results

Question

NDSolve producing very oscillatory solutions even after not having any large numbers or warning/errors

A1 = NDSolve[{P'[x] + (P[x] + Q[x])^(1/2)* P[x] == -10^3 P[x] - 
 P[x]^2, Q'[x] + (P[x] + Q[x])^(1/2)* Q[x] == 10^3 P[x] + P[x]^2, 
P[0.1] == 10^-3, Q[0.1] == 10}, {P[x], Q[x]}, {x, 0.1, 10^5}]
LogLogPlot[{P[x]/(P[x] + Q[x])} /. A1, {x, 0.1, 10^5}, PlotRange -> Full, PlotPoints -> 1000]

score 2 · Answer 1 · answered Nov 17 '23 at 08:58

2

If you plot result in a smaller timerange (not LogLogPlot)

Plot[{P[x]/(P[x] + Q[x])} /. A1, {x, .1,  .111 } , PlotRange -> All ]

you see that result vanishes very fast. No need to use a huge simulation range 0.1...10^5!

answered Nov 17 '23 at 08:58

Ulrich Neumann

53,729
2
23
55

However, the challenge arises when I have to solve it for a larger range, that’s where I encounter the problem and need help – user105697 Nov 17 '23 at 09:07
Your "challenge" is to observe a very small result( << WorkingPrecision) for a long time? Then you should adapt WorkingPrecision! – Ulrich Neumann Nov 17 '23 at 09:17

rhermans · Answer 2 · 2023-11-17T10:46:17.143

Read Numerical Operations On Functions

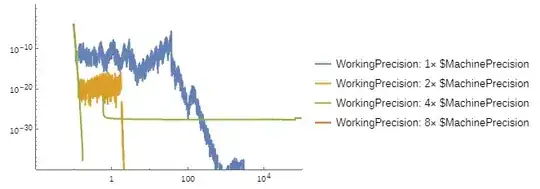
When you work numerically, you should always ask yourself if the results depend or not on your working precision (WorkingPrecision).

You should only trust calculations that are stable with respect to the parameters used for the discretization of the problem.

Particularly with WorkingPrecision, it should be high enough that small changes in WorkingPrecision will give similar results, with variations within your acceptable tolerances.

In your case clearly, you are looking at an artefact of poor parameters for the discretization, like the small default (WorkingPrecision), as the results look different for different choices for WorkingPrecision values.

Check other options like: MaxStepFraction, MaxSteps, MaxStepSize, Method, PrecisionGoal, StartingStepSize, etc.

LogLogPlot[
    Evaluate[
        ReplaceAll[
            P[x]/(P[x] + Q[x]), 
            First@NDSolve[
                {
                    P'[x] + (P[x] + Q[x])^(1/2)* P[x] == -10^3 P[x] - P[x]^2, 
                    Q'[x] + (P[x] + Q[x])^(1/2)* Q[x] == 10^3 P[x] + P[x]^2,
                    P[0.1] == 10^-3, Q[0.1] == 10
                }
        , { P[x], Q[x] }
        , { x, 0.1, 10^5 }
        , WorkingPrecision->#*$MachinePrecision
        ]
        ]& /@ Echo@PowerRange[1,8,2]
    ]
    , {x, 0.1, 10^5}
    , PlotRange -> {{10^-2,10^5},{10^-40, 10}}
    , PlotPoints -> 1000
    , PlotLegends->Evaluate[Row[{"WorkingPrecision: ",  #, "\[Times] $MachinePrecision"}]& /@ PowerRange[1,8,2]]
]

Thank you for pointing out this fact, but the solution still exhibits discontinuities, which I am unable to overcome. — user105697, Nov 17 '23 at 10:44
@user105697 Show me that your results are stable with respect to your discretization parameters first, and then we can discuss the results. Until then, we are looking at artefacts of the bad integration. A false premise may lead to false conclusions. Here you are abusing the premise that the numerical integration is a good approximation of the real result. — rhermans, Nov 17 '23 at 10:48
@user105697 "discontinuities" are caused by LogLogPlot because simulation result is sometimes negativ. — Ulrich Neumann, Nov 17 '23 at 14:55

score 2 · Answer 3 · answered Nov 17 '23 at 11:40

There are several problems posed in Your Mathematica built-ins parameter set.

The Plot built-in is used correctly.

The NDSolve built-in is not.

Solving numerically for differential equation is only local not global. So $10^5$ is a universe for a solution is it is already having gaps at value in the range of $10^-1$.

The results are very small numbers so altering the precision is very adequate.

If NDSolve detects small values or no changes or only small changes than a correction algorithm is used to generate some change. For example the step length is increase or other pivotal routine is set to operation. This differential equation drops rapidly to very small value so this is for sure a dance made by NDSolve internal operations only and not a signature of the given differential equation at all.

Mathematically this is not oscillatory any more. Technical this might be called noise. But it is a background noise. I read recently a review calling this residual numerical noise. It is a property of NDSolve not of the tranquility of the given mathematical or technical problem.

This looks somehow like the plot of the error that is generated by NDSolve if certain Mathematica built-ins are used. That is because it is getting smaller with the time the process of solving is continued.

My reproductions shows this picture:

This is a already given answer for more of the posed problems if taken seriously: error control for NDSolve. I state this is under this consideration not a duplicate of this question.

The noise shown looks more second order like on this How to increase NDSolve accuracy for 2nd order ODE? pictures and thereby the rhetorics change to accuracies. The phenomenological style posed is not leading or pointing into solutions directions.

Since Mathematica treads such problems in the complex numbers such dropouts are usual. Look at the complex plots of the solution instead for more continuations.

Hope that helps for further steps or is already solution enough and suffices.

NDSolve producing oscillatory results

3 Answers3