The OP's -- oops, they're bbodfrey's -- pictures suggest the problem is with interpolation, as bbgodfrey also observed. Some of the problem can be ameliorated with the InterpolationOrder option.
From InterpolationOrder:
In functions such as NDSolve, InterpolationOrder->All specifies that the interpolation order should be chosen to be the same as the order of the underlying solution method.
Another problem is that NDSolve seems to have trouble at the beginning of the integration. This sometimes can be dealt with the StartingStepSize option.
It can also be dealt with by differentiating the differential equation.
To get a precision of 30 digits, WorkingPrecision usually needs to be at least twice as large or 60, and PrecisionGoal and AccuracyGoal need to be at least 30 -- a little higher is usually needed get strictly at least 30 digits. By default, these are set to half of WorkingPrecision. In some cases, the MaxStepSize option is needed to keep NDSolve from getting too ambitious and committing an "NDSolve::nderr: Error test failure".
The following three approaches give results with a residual error of less than 10^-30 throughout the interval of integration.
{rsol} = NDSolve[
{(R'[t])^2 + 2 R[t] R''[t] == -1, R[1] == 1, R'[1] == 2/3},
R, {t, 1, 3},
Method -> "ExplicitRungeKutta", WorkingPrecision -> 61,
InterpolationOrder -> All];
diffeq = (R'[t])^2 + 2 R[t] R''[t] == -1;
{rsol} = NDSolve[
{D[diffeq, t],
{R[1], R'[1], R''[1]} ==
({R[t], R'[t], R''[t]} /. First@Solve[diffeq, R''[t]] /. {R[t] -> 1, R'[t] -> 2/3})},
R, {t, 1, 3},
MaxStepSize -> 3*^-4, WorkingPrecision -> 62,
InterpolationOrder -> All];
{rsol} = NDSolve[
{(R'[t])^2 + 2 R[t] R''[t] == -1, R[1] == 1, R'[1] == 2/3},
R, {t, 1, 3},
StartingStepSize -> 1*^-8, MaxStepSize -> 1*^-4,
PrecisionGoal -> 33, AccuracyGoal -> 33, WorkingPrecision -> 70,
MaxSteps -> 2*^5, InterpolationOrder -> All];
The first one ("ExplicitRungeKutta") produces the smallest (memory use) solution (2.5s, 3.4MB). The second (differentiating the ODE) is fastest with excellent precision control (1.5s, 43MB). And the third, well, it works, and after it gets started is the most accurate (3.4s, 89MB).
Plot[
(R'[t])^2 + 2 R[t] R''[t] + 1 /. rsol // RealExponent // Evaluate,
{t, 1, 3}, PlotRange -> All, WorkingPrecision -> 70]

The Runge-Kutta solution.

Differentiating the differential equation.

Controlled step size.
You might notice that the largest error is near the beginning (in all cases). The interesting stuff around t == 2.5 is where the first derivative is zero.



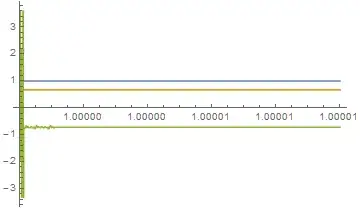
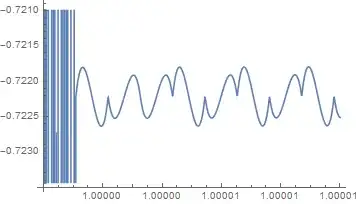
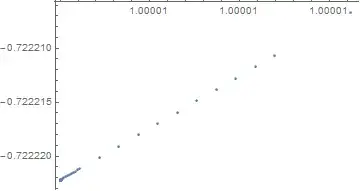


StartingStepSize,WorkingPrecisionto play with. The problem seems to be at the start. It usually does not help much to increasePrecisionGoalandAccuracyGoalunless you also increaseWorkingPrecision. What error would be acceptable? SinceNDSolvecomputes discrete steps, you should expect the error oscillate between the steps (but only a small amount). Having zero error throughout is not really an achievable goal. – Michael E2 Jul 22 '15 at 01:43