Generating an "average curve" from a dense set of "semicontinuous curves" which clear trends

Question

This question is related to a previous one of mine: Partitioning a superset of coordinates into subsets that generate continuous curves, where the challenge was to partition a data set into two clusters representing distinct "semicontinuous curves" (we mean this in the loose sense that a ListPlot generated two curves that by eye appeared to be continuous). The user rm -rf illustrated and demonstrated that FindClusters could very nice solve the problem using a Euclidean distance metric (a hat tip also to g3kk0 who elaborated on this approach).

My question here is how one would approach a much more pathological case, where we have multiple closely spaced curves, displaced some amount vertically, and we would like to generate an "average" curve that represents a sort of average for the shape of all the semicontinuous curves.

Take a look at the following plots (data uploaded to: https://www.dropbox.com/sh/751invayqe3ip9b/r6raIrdvLF):

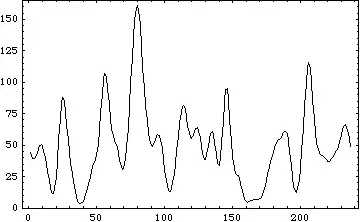
Plot A:

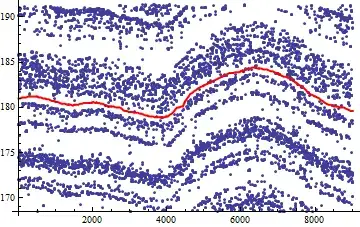
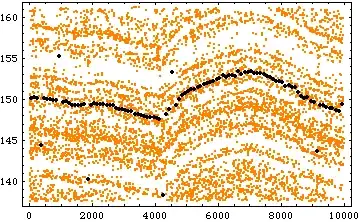
Plot B:

In both cases, we can more or less clearly make out by eye what the shape of each semicontinuous curve looks like. For example, take the following "hand drawn" traces of two semicontinuous curves in Plot B:

While it may not be possible to separate the data sets for Plot A and Plot B into clusters that represent each of these semicontinuous curves (I'd love to be corrected on this point), how can we automatically generate a sort of "average curve" that follows the trend for each of the semicontinuous curves?

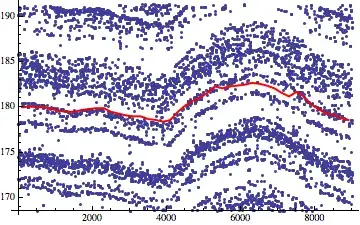
Update: In reponse to rm -rf's comment, if we take a similar data set to Plot B and bin along the X-axis and then compute a mean for each bin (computing the median generates a similar result), the resulting plot looks like this:

My explanation for this is that we cannot "see" (i.e. we do not have access to) all of the semicontinuous curves in the plot. A peak in the set of curves may cause additional curves to appear near the bottom of the plot (see the $X \approx 5000$ to $8000$ region in Plot B), and vice versa.

---

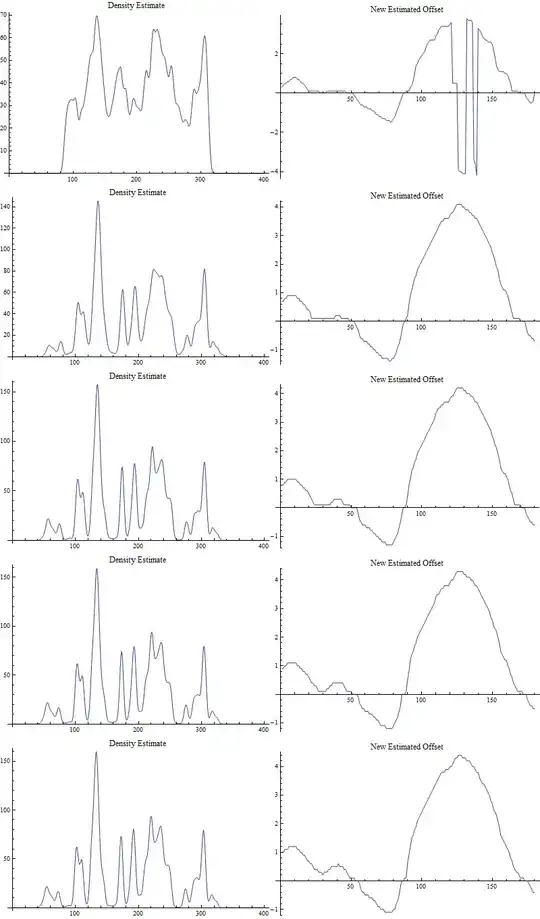
Update 2: If we connect all points within some small cutoff distance $T$ (perhaps $T = 1$ here), generating a random geometric graph, perhaps we could look at the angle of the edges connecting the points / vertices? This shouldn't be affected very much by the presence of peaks or troughs of curves at the bottom and top of the plot, respectively.

---

Update 3: Provided that the data here is generally periodic along the $y$-axis, it might be reasonable to treat the surface as if it it curves around on itself like a tube (where the x-axis is the long-axis of the tube, and the curvature occurs along the y-axis).

Answer 1

Your data seems to be composed of two components: An offset for each x-location (or an offset-function of x) and a density relative to that offset. If you had either of the two, estimating the other would be easy. Right so far?

One common solution for this kind of problem is the EM algorithm. Basically, you start with some estimate for one variable (e.g. the offset function) and use that to update the other (the density). Then you use fix the density and update the offsets. Rinse and repeat.

I used your "B" dataset for testing:

data = ToExpression[
   Import["https://dl.dropboxusercontent.com/sh/751invayqe3ip9b/\
lhJ65LVWMI/Plot%20B%20Points.txt?token_hash=AAF1qneRm1kbtw4P9p_\
JCMhzO1SpmMlDst8zMbLfG_cNjQ&dl=1"]];

I need some parameters for estimating the density given the offsets and estimating the offsets given a density, but the algorithm is (relatively) robust to different parameters:

histogramBinSize = 0.1;
partitionSize = 50;
filterSize = 5;

makeHist = 
  Function[data, 
   GaussianFilter[BinCounts[data, {160, 200, histogramBinSize}], 
    filterSize]];

makeHist estimates the density from a set of values (with offsets removed).

The EM step takes an estimate for the offset at each position, calculates a denstiy estimate and returns a new offset estimate from that:

emStep = Function[offsetEstimate,
   Module[{densityEstimate, zeroMeanDensityEstimate, correlation, 
     shift, offsets, offsetForEachPoint, dataWithoutOffset, 
     newDensityEstimate},
    (
     (* first estimate the density *)
     dataWithoutOffset = data - offsetEstimate;
     densityEstimate = makeHist[dataWithoutOffset];

     (* then estimate the offset given the density, using simple correlation *)
     zeroMeanDensityEstimate = densityEstimate - Mean[densityEstimate];
     correlation = 
      GaussianFilter[
       ListCorrelate[zeroMeanDensityEstimate, makeHist[#], 1] & /@ 
        Partition[data, partitionSize], filterSize];
     shift = Round[Length[densityEstimate]/2];
     offsets = 
      histogramBinSize (Position[RotateRight[#, shift], Max[#]][[1, 
            1]] - shift) & /@ correlation;
     offsetForEachPoint = 
      ListInterpolation[offsets, {1, Length[data]}, 
        InterpolationOrder -> 1][Range[1, Length[data]]];

     Sow[
      Row[
       {
        ListLinePlot[densityEstimate, PlotLabel -> "Density Estimate",
          ImageSize -> 400],
        ListLinePlot[offsets, PlotLabel -> "New Estimated Offset", 
         ImageSize -> 400]
        }]];

     offsetForEachPoint
     )]];

Starting with offset 0 for each point, the algorithm converges to a good estimate after a few iterations:

offsetStart = data*0;
{offsetEstimate, {output}} = Reap[Nest[emStep, offsetStart, 5]];
Show[ListPlot[data], 
 ListLinePlot[180 + offsetEstimate, PlotStyle -> {Red, Thick}]]

The EM step sows a plot of the current offset/denstiy estimate after each iteration. As you can see, it converges to a good solution quite quickly:

Column[output]

There are several ways to improve this simple algorithm:

• You could probably come up with a smarter way to estimate the density given the offsets.
• The estimation of the offset given the density is also far from perfect (it just looks for the maximum correlation at each x-location). For example, you could only search for offset functions without large jumps (e.g. Viterbi's or some graph-path-searching algorithm. Or maybe some general function approximation like Gaussian Process).
• The algorithm is still quite ad-hoc. You could probably improve the results and/or automatically optimize the parameters by treating the "densities" as proper probability densities and estimating real probabilities (instead of a meaningless correlation score).

Update: To process the "multiple values per column" dataset, I'd change the data format a little so it can be processed by the same algorithm:

data2d = ToExpression[
   Import["https://dl.dropboxusercontent.com/sh/751invayqe3ip9b/\
Ra8vDwQ1Ew/DataSet%20-%20Multiple%20Points%20Per%20Column.txt?token_\
hash=AAF1qneRm1kbtw4P9p_JCMhzO1SpmMlDst8zMbLfG_cNjQ&dl=1"]];

data = Flatten /@ data2d[[All, All, 2]];

Now data contains an array of y-values for each x-column, i.e. when data2d looks like this,

{{}, {{2, 149.645}}, {{3, 149.533}}, {{4, 139.979}}, {{5, 
   156.648}, {5, 140.324}}, {{6, 139.452}}, {{7, 145.777}, {7, 
   140.795}, {7, 138.106}}, {{8, 145.766}, {8, 140.788}, {8, 
   137.636}} ...

data will look like this:

{{}, {149.645}, {149.533}, {139.979}, {156.648, 140.324}, 
 {139.452}, {145.777, 140.795, 138.106}, {145.766, 140.788, 137.636}...

There are really only three kinds of operations I do with the data:

• Calculate a histogram of all points,
• Partition it into N-column stripes and calculate a histogram for each
• Subtract an offset-list containing an offset for each x-column

All of these work perfectly well for a list of values for each column, as long as the histograms are calculated from a flattened list:

makeHist = 
  Function[data, 
   GaussianFilter[
    BinCounts[Flatten[data], {130, 170, histogramBinSize}], 
    filterSize]];

And I had to adjust the final data display:

Show[ListPlot[Flatten[data2d, 1]], 
 ListLinePlot[Mean[Flatten[data]] + offsetEstimate, 
  PlotStyle -> {Red, Thick}]]

Other than that, the algorithm works fine for this dataset:

Answer 2

Here's some code implementing the purely local strategy suggested in my comment.

points = << "~/tmp/Plot B Points.txt";
xwidth = 200;
ywidth = 0.1;
binnedPoints = Partition[points, xwidth];
histograms = BinCounts[#, {Min@points, Max@points, ywidth}] & /@ binnedPoints;
align[a_, b_] := First@Ordering[ListCorrelate[a, b, {-1, 1}, 0], -1] - Length@a;
x = Table[xwidth (i - 1/2), {i, Length@binnedPoints}];
y = ywidth ({0}~Join~Accumulate[align[#[[1]], #[[2]]] & /@ Partition[histograms, 2, 1]]);
Show[ListPlot[points], 
 ListPlot[Transpose@{x, 180 + y}, PlotStyle -> {Thick, Red}, Joined -> True]]

All the work is done by the align function, which finds the offset at which the two lists have the greatest inner product.

This approach is a little fiddly in that (i) you have to pick xwidth and ywidth carefully to get sensible results, (ii) if it chooses the wrong alignment somewhere along the way, it will not recover, and (iii) it has a fair amount of drift even for the reasonable-looking range of $0\le x\le4000$.

(P.S. Actually, for xwidth = 300 it does a near-perfect job on both data sets A and B. But I want to leave this result here as it clearly shows the limitations of this method. Try xwidth = 200 on data set A to see it really screw up.)

Answer 3

Here's a more "signal processing" approach using the MeanShiftFilter. This filter averages the data in two dimensions, first in terms of the range (in this case, how far up or down the plot) and the other in terms of the value (in this case, they are all the same, so no averaging occurs). Because it's hard to guess what good filtering parameters might be, it is convenient to set it up as a Manipulate:

data = ToExpression[Import["http://pastebin.com/raw.php?i=49NWMxgK"]];
Manipulate[ListPlot[Nest[MeanShiftFilter[#, range, 2] &, data, iter]], 
     {range, 1, 200, 2}, {iter, 1, 50, 1}]

where data is the data as given in the OPs problem statement (as uploaded to pastebin by rm-rf). Here is the output with parameters doing no filtering:

and here it is with the sliders adjusted to show some of the major trend lines:

The only trick used here is to iterate the filtering a number of times, as controlled by the slider labelled iter, and implemented using the Nest function. As an alternative, qualitatively similar answers result from using the BilteralFilter. For this example, the mean-shift looked a little better, but on other data it might be worth trying.

Answer 4

I tried to implement nikie's code but I never got it running, perhaps because I use version 5.2 and may have messed up my implementation of some now-built-in function. In any case, I gave up and started from scratch. I followed the same general approach, but with a couple twists that I think justify this post.

First, I bin and smooth only once, before starting the EM iterations. All the shifting to align a distribution with the overall distribution is done to the y-bins themselves. Second, each "shift" is actually a rotation: the upper bound of the top y-bin is just above the highest y-value in the data, the lower bound of the bottom y-bin is just below the lowest y-value, and bins that are shifted off one end of the distribution reappear at the other end

Here is the code. It expects the data to be organized as in the "Multiple Points Per Column" data set. The data in "desktop/multiple", used below, was downloaded manually (copy/paste) from "http://pastebin.com/raw.php?i=UaCWU5Pv".

data = <<"desktop/multiple";
xy = Flatten[data,1];
xyy = {#[[1,1]],#[[All,2]]}& /@ (data/.{}->Sequence[]);
{x,yy} = Transpose@xyy;
{xmin,xmax} = x[[{1,-1}]];

(* first the x-binning *)

nominalXbinSize = 100;
nXbins = Round[(xmax-xmin+1)/nominalXbinSize];
XbinAssignments = Ceiling[(x-xmin+1)*nXbins/(xmax-xmin+1)] + xmin-1;
XbinSizes = Length/@Split@XbinAssignments;
XbinBounds = Transpose@{Most@#+1,Rest@#}&[FoldList[Plus,0,XbinSizes]];
yData = Flatten@Take[yy,#]& /@ XbinBounds;

(* then the y-binning *)

nominalYbinSize = .10;
{ymin,ymax} = {Min@#,Max@#}&[y = xy[[All,2]]];
{dmin,dmax} = {Min@#,Max@#}&[Rest@#-Most@#&@Union@y];
nYbins = Round[(ymax-ymin+dmin)/nominalYbinSize];
YbinSize = (ymax-ymin+dmin)/nYbins;
bData = Ceiling[(yData-ymin+.5dmin)/(ymax-ymin+dmin)*nYbins];

(* Each row of bData contains the y-bin numbers of the yData for an x-bin.
   Convert each row to a “smoothed” frequency table,
   using the defaults from the built-in (v7+) GaussianFilter. *)

radius = 5;
filter = #/Tr@#&@BesselI[Range[-radius,radius],(.5*radius)^2];
smoothFreqs = ListCorrelate[filter, Normal@SparseArray[
  #[[1]] -> Length@#& /@ Split@Sort@#, nYbins], radius+1]& /@ bData

(* Initialize, then drop into the EM loop.
   Iterate until no further rotation is needed. *)

cumrot = Table[0,{nXbins}]; density = Total[rotFreqs = smoothFreqs]; iter = 0;
Timing[ While[ Max@Abs[rotvec = Append[Mod[First@Ordering[ ListCorrelate[
density,#,1],-1]&/@Most@rotFreqs - 1, nYbins, (1-nYbins)/2 ], 0]] > 0,
density = Total[rotFreqs = MapThread[RotateLeft[##]&,{rotFreqs,rotvec}]];
cumrot += rotvec; iter++]; ToString@iter<>" EM steps"]

(* Done. Display the results. *)

cumrot = Mod[cumrot, nYbins, (1-nYbins)/2 ];
ListPlot[density,PlotRange->All,Frame->True,Axes->None, PlotJoined->True];
ListPlot[xy, PlotRange->All, Frame->True, Axes->None, Prolog->Orange, Epilog->{Black,
PointSize[.015], Point/@Transpose@{#1.#2/Tr@#2&@@{Take[x,#],Length/@Take[yy,#]}&
  /@XbinBounds,.5(ymax+ymin)+YbinSize*cumrot}}];
SequenceForm["Nominal X-bin size = ", nominalXbinSize,
  "\nNominal Y-bin size = ", nominalYbinSize, "\nFilter radius = ", radius]

{0.44 Second, 22 EM steps}

Nominal X-bin size = 100
Nominal Y-bin size = 0.1
Filter radius = 5