Colouring the "leaves" (self-intersections) of parametric curves

Question

I want to emphasize the self-intersections ("leaves") of parametric curves by applying a pattern or color to them.

Using cvgmt's answer to this question:

how-to-separate-the-regions-enclosed-by-curves

We define:

MeshComponents[plot_, n_, d_] :=
 Module[{mc},
  mc = RegionDistance[DiscretizeGraphics @ plot];
  mc = ImplicitRegion[mc @ {x, y} >= d, {{x, -n, n}, {y, -n, n}}];
  mc = BoundaryDiscretizeRegion[mc,
    Method -> "Semialgebraic",
    MaxCellMeasure -> 0.01];
  ConnectedMeshComponents @ mc]

We also define

$fill = PatternFilling["Diamond", ImageScaled[1/30]];

and

ColorLeaves[plot_, n_, d_, del_] :=
 Module[{mc, cl},
  mc = Delete[List /@ del] @ MeshComponents[plot, n, d];
  cl = Transpose[{Array[$fill &, Length @ mc], mc}];
  Show[Graphics[cl, Axes -> True], plot]]

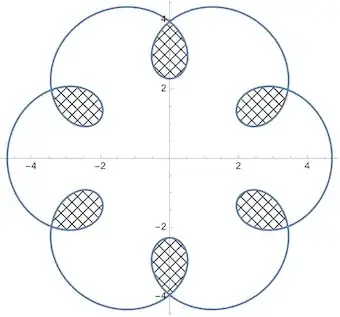
Filling the leaves of an Epitrochoid is now relatively easy:

fun = 
 {a Sin[u] - b Sin[2 a u], a Cos[u] - b Cos[2 a u]} /. {a :> 3.5, b :> 1.2};
plot = ParametricPlot[fun, {u, 0, 2 Pi}];
MeshComponents[plot, 5, 0.025]

To only select the leaves we have to delete the first and third component.

ColorLeaves[plot, 5, 0.025, {1, 3}]

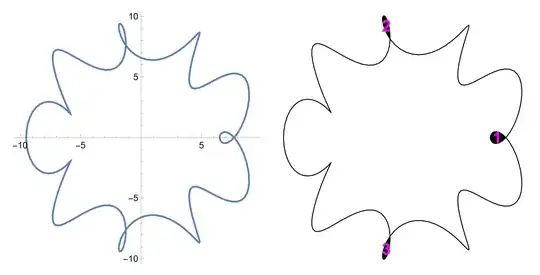
We use the same procedure to colour two other curves:

$fill = FaceForm[ColorData[97, "ColorList"][[2]]];
fun =
  {Cos[u] (a Sin[u]^b + 1)/a, -Sin[u] (a Cos[u]^c + 1)/a} /. {a :> 3, b :> 3, c :> 2};
plot = ParametricPlot[fun, {u, 0, 2 Pi}];

Looking at its mesh components we see that the 1st and 4th component must be deleted.

ColorLeaves[plot, 1, 0.0025, {1, 4}]

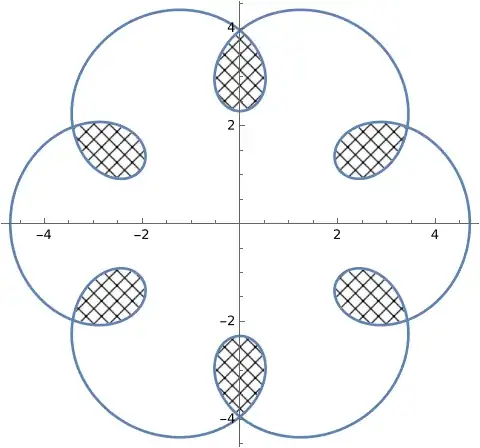
Similarly with the next plot:

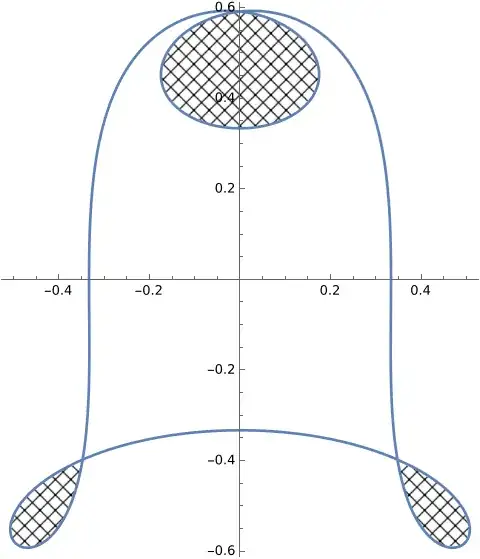
fun = {Sin[u], -Cos[u]} Cos[u] (4 Sin[u]^2 - 1);
plot = ParametricPlot[fun, {u, 0, 2 Pi}];
ColorLeaves[plot, 1, 0.0025, {2}]

My question

It is cumbersome to visually inspect the mesh components for each curve and select the right ones. How can this process be automated? I need a short function which automatically detects the roundish leave-like shapes and ignores the other ones.

Thank you in advance for your suggestions and a Happy New Year for all of you

It is recommended to rewrite the code MeshComponents as below that we need not set the rangement n manually. Clear[MeshComponents]; MeshComponents[plot_, d_] := Module[{reg, bd, dist, mc, imreg}, reg = DiscretizeGraphics@plot; bd = RegionBounds[reg]; dist = RegionDistance[reg]; imreg = ImplicitRegion[dist@{x, y} >= d, {x, y}]; mc = BoundaryDiscretizeRegion[imreg, ScalingTransform[1.2*{1, 1}, Mean /@ bd]@bd, Method -> "Semialgebraic", MaxCellMeasure -> 0.01]; ConnectedMeshComponents@mc], after that , the code by @kglr work for the complex cases. — cvgmt, Jan 03 '24 at 01:40

cvgmt · Accepted Answer · 2024-01-02T05:51:28.167

It seems that https://mathematica.stackexchange.com/a/295351/72111 with RegionDisjoint work for all the cases.
Here we test the more complex cases fun = 8 {Cos[u], Sin[u]} - 2.5 {Cos[10 u], Sin[8 u]};

Clear["Global`*"];
fun = 8 {Cos[u], Sin[u]} - 2.5 {Cos[10 u], Sin[8 u]};
$fill = PatternFilling["Diamond", ImageScaled[1/30]];
plot = ParametricPlot[fun, {u, 0, 2 [Pi]}, PlotPoints -> 60, 
   MaxRecursion -> 2];
lines = Cases[plot, _Line, -1] // First;
data = RegionMeshSplitIntersectingSegments[lines];
pts = data[[1]];
splits = data[[2]];
segments = Flatten[Partition[#, 2, 1] & /@ splits, 1];
g = Graph[Range@Length@pts, UndirectedEdge @@@ segments, 
   VertexCoordinates -> pts];
faces = PlanarFaceList[g];
polys = Polygon[pts[[#]]] & /@ faces;
polys = Pick[polys, Or @@@ Outer[RegionDisjoint, polys, polys]];
polys = DeleteDuplicates[polys, RegionEqual];
Graphics[{lines, {$fill, polys}, Magenta, 
  MapIndexed[Text[Style[First@#2, 18, Bold], RegionCentroid@#1] &, 
   polys]}]

For

fun = 8 {Cos[u], Sin[u]} - 1.5 {Cos[8 u], Sin[10 u]};

score 8 · Answer 2 · answered Jan 01 '24 at 22:53

ClearAll[meshLeaves]

meshLeaves = GraphComputation`SinkVertexList @
  RelationGraph[UnsameQ @ ## && 
       RegionWithin[BoundingRegion[#], BoundingRegion[#2]] &, 
     MeshComponents[##]] &;

Examples:

$fill = PatternFilling["Diamond", ImageScaled[1/30]];
fun1 = {a Sin[u] - b Sin[2 a u], 
    a Cos[u] - b Cos[2 a u]} /. {a :> 3.5, b :> 1.2};
plot1 = ParametricPlot[fun1, {u, 0, 2 Pi}];
Show[Graphics[{$fill, meshLeaves[plot1, 5, 0.025]}, Axes -> True], plot1]

fun2 = {Cos[u] (a Sin[u]^b + 1)/a, -Sin[u] (a Cos[u]^c + 1)/a} /. {a :>
      3, b :> 3, c :> 2};
plot2 = ParametricPlot[fun2, {u, 0, 2 Pi}];
Show[Graphics[{$fill, meshLeaves[plot2, 1, 0.0025]}, Axes -> True], plot2]

fun3 = {Sin[u], -Cos[u]} Cos[u] (4 Sin[u]^2 - 1);
plot3 = ParametricPlot[fun3, {u, 0, 2 Pi}];
Show[Graphics[{$fill, meshLeaves[plot3, 1, 0.0025]}, Axes -> True], plot3]

Colouring the "leaves" (self-intersections) of parametric curves

2 Answers2

Linked