The method by @halmir also work for this case.
https://mathematica.stackexchange.com/a/267223/72111
Clear["Global`*"];
eqns = {x^2 + y^2 - 16 == 0, (x - 2)^2 + (y + 1)^2 - 9 == 0,
x^2/36 + y^2 == 1};
plot = ContourPlot[eqns // Evaluate, {x, -20, 20}, {y, -20, 20},
MaxRecursion -> 2, PlotPoints -> 50];
lines = Cases[Normal@plot, _Line, -1];
data = Region`Mesh`SplitIntersectingSegments[lines];
pts = data[[1]];
splits = data[[2]];
segments = Flatten[Partition[#, 2, 1] & /@ splits, 1];
g = Graph[Range@Length@pts, UndirectedEdge @@@ segments,
VertexCoordinates -> pts];
faces = PlanarFaceList[g];
polys = Polygon[pts[[#]]] & /@ faces;
polys = Delete[polys, First@Ordering[Area@polys, -1]];
colors = ColorData[97] /@ Range@Length@polys;
GraphicsRow[{Graphics[{RandomColor[], #} & /@ lines],
Graphics[Thread[{colors, polys}]]}]

- Test several arbitrary curves.
Clear["Global`*"];
lines = Table[
BSplineFunction[RandomReal[1, {10, 2}]] /@ Subdivide[200] // Line,
3];
data = Region`Mesh`SplitIntersectingSegments[lines];
pts = data[[1]];
splits = data[[2]];
segments = Flatten[Partition[#, 2, 1] & /@ splits, 1];
g = Graph[Range@Length@pts, UndirectedEdge @@@ segments,
VertexCoordinates -> pts];
faces = PlanarFaceList[g];
polys = Polygon[pts[[#]]] & /@ faces;
colors = ColorData[97] /@ Range@Length@polys;
GraphicsRow[{Graphics[{RandomColor[], #} & /@ lines],
Graphics[Thread[{colors, polys}]]}]
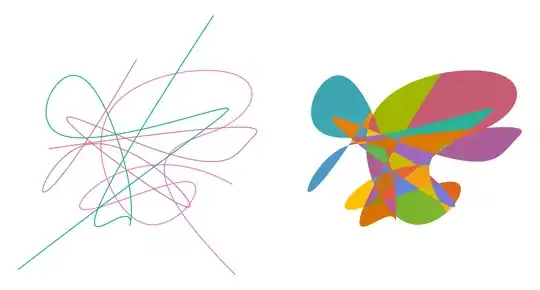
- We use
WindingCount to remove the largest face.
Clear["Global`*"];
eqns = {x^2 + y^2 - 16 == 0, (x - 2)^2 + (y + 1)^2 - 9 == 0,
x^2/36 + y^2 == 1};
plot = ContourPlot[eqns // Evaluate, {x, -20, 20}, {y, -20, 20},
MaxRecursion -> 2, PlotPoints -> 50];
lines = Cases[Normal@plot, _Line, -1];
reg = DiscretizeGraphics /@ lines // RegionUnion;
g = Graph[MeshPrimitives[reg, 1] /. Line -> Apply@UndirectedEdge,
VertexCoordinates -> MeshCoordinates[reg]];
faces = PlanarFaceList[g];
faces = Select[faces, WindingCount[Line@#, Mean@#] == 1 &];
GraphicsRow[{Graphics@lines,
Graphics[{{RandomColor[], Polygon@#} & /@ faces}]}]
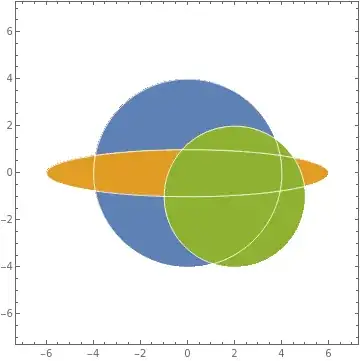
- Add the dual grah.But I don't know why there are multiple edges in the dual planar graph.
Clear["Global`*"];
SeedRandom[123];
eqns = {x^2 + y^2 - 16 == 0, (x - 2)^2 + (y + 1)^2 - 9 == 0,
x^2/36 + y^2 == 1};
plot = ContourPlot[eqns // Evaluate, {x, -20, 20}, {y, -20, 20},
MaxRecursion -> 2, PlotPoints -> 50];
lines = Cases[Normal@plot, _Line, -1];
reg = lines // RegionUnion;
g = Graph[MeshPrimitives[reg, 1] /. Line -> Apply@UndirectedEdge,
VertexCoordinates -> MeshCoordinates[reg]];
faces = PlanarFaceList[g];
index = FirstPosition[WindingCount[Line@#, Mean@#] & /@ faces, -1];
faces2 = Delete[faces, index // First];
graphics2 = Graphics[{{RandomColor[], Polygon@#} & /@ faces2}];
dual = Graph[VertexList@DualPlanarGraph[g],
EdgeList@DualPlanarGraph[g],
VertexCoordinates -> RegionCentroid@*Polygon /@ faces,
EdgeStyle -> White, VertexStyle -> White,
VertexSize -> Automatic];
dual2 = VertexDelete[dual, VertexList[dual][[First@index]]];
Show[graphics2, dual2]








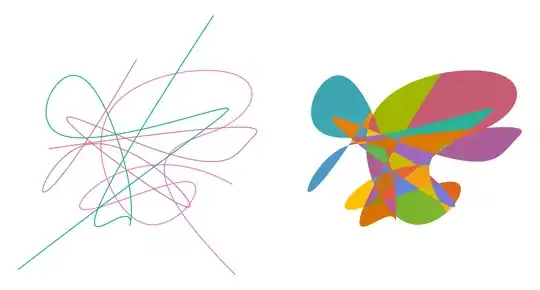




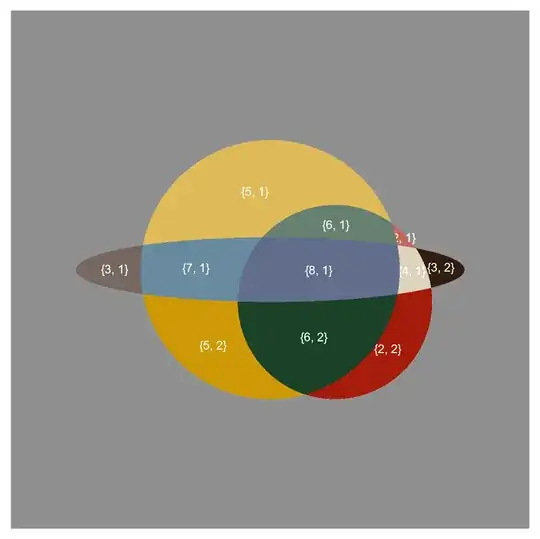
A, B, CuseImplicitRegionfor each of your equations. – Syed Dec 22 '21 at 07:57