Mathematica and WolframAlpha incorrectly simplified $\frac{\lfloor x\rfloor}{\lfloor x\rfloor}$ to 1, why?

Question

Consider the following limit:

$$\large\lim_{x\to 0^+}\frac{\lfloor x\rfloor}{\lfloor x\rfloor}$$

The domain of the function $f(x) = \frac{\lfloor x\rfloor}{\lfloor x\rfloor}$ is $\mathbb{R}-[0, 1)$. This shows that the limit of this function as $x$ approaches zero from right, does not exist because to calculate this limit, the function needs to be defined on an open interval such as $(0, 1)$, which, according to the domain of the function, is not the case.

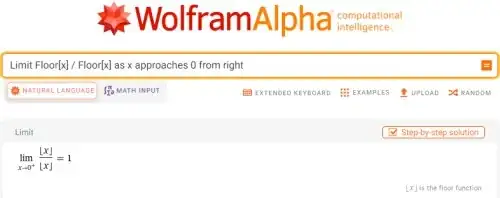
Everything looks well and logical, but if you calculate this limit in Wolfram Mathematica, you will see:

Why is this?! And, of course, in WolframAlpha.com, you will also see the same result.

You can also see this at HERE.

Why is this?

I realized that Mathematica and WolframAlpha incorrectly simplified $\frac{\lfloor x\rfloor}{\lfloor x\rfloor}$ to 1; why?? (While we know that this is incorrect because it is like saying that the two functions $f(x) = \frac{\lfloor x\rfloor}{\lfloor x\rfloor}$ and $g(x)=1$ are equal, which is not the case)

Answer 1

More of an extended comment than an answer...

While many people view Mathematica as a magic doer-of-all-things-mathematical, it is fundamentally a programming language. It's a programming language with specific execution rules. At some point in using Mathematica, understanding the paradigm of the underlying programming language becomes crucial to understanding results and to crafting good inputs.

The short explanation here is that Limit never actually encounters the expression Floor[x]/Floor[x]. If Limit had one of the Hold* attributes, then maybe it could be made to deal with these kinds of situations, but it doesn't. So, by the time Limit "sees" its arguments, the situation looks like this (as has been pointed out by Nasser):

Limit[1, x -> 0, Direction -> "FromAbove"]

(Side note, Trace is a very useful function to help you understand the evaluation process.)

Okay, you say, but Floor[x]/Floor[x] shouldn't be assumed to evaluate to 1. But Mathematica doesn't see functions, just expressions. You could make the same argument that a/a shouldn't evaluate to 1 (assuming that a itself is a symbol with no definitions attached), because we don't know that the "variable" a can't be 0, but it does in fact evaluate to 1. That's part of the evaluation rules.

All of this is entirely by design. It might be frustrating. It might be different than what you want or expect, but this is just an inherent part of how the language works and how Limit and Divide were designed.

There are going to be situations where you need to guide the language to do what you want. For example, you've said

The domain of the function ()=⌊⌋/⌊⌋ is ℝ−[0,1)

but there is no way for Mathematica to know that. To Mathematica, there are no actual functions, just expressions and evaluation rules. And there is no general way for it to infer constraints on expressions that you can always rely on. You as the designer of the program must provide a complete specification. Maybe something like this:

f[x_] := Piecewise[{{Floor[x]/Floor[x], x >= 1 || x < 0}}, Indeterminate]

Now we can try the limit:

Limit[f[x], x -> 0, Direction -> "FromAbove"]

This returns unchanged (from Limit's point of view, f[x] actually evaluated, replacing the Floor expression with just 1), which seems reasonable to me because now it's obvious that the limit expression was improper.

If there is any complaint to be had here, it's with Wolfram Alpha. It could maybe be argued that as an educational tool (if that is indeed its purpose) it should do some pre-parsing to inspect the input for problematic cases. But I'm not very familiar with Wolfram Alpha, so I can't really infer any design intentions.

Answer 2

As was already pointed out in one comment and in one answer that the result obtained was correct but incorrect was assumption of OP how Mathematica works or how it should work.

I just want to present another example of code that illustrates how Mathematica works in this case:

First notice that

FullSimplify[x^2 + 3 x + 1 - (x + 1)^2] === x

---

True

So we can use Floor[x^2 + 3 x + 1 - (x + 1)^2]] instead of one of Floor[x].

Table[Limit[Floor[x^2 + 3 x + 1 - (x + 1)^2]/Floor[x], x -> p, 
    Direction -> #] & /@ {"FromBelow", "FromAbove"}, {p, 0, 1, 1/10}]

---

{{1, Indeterminate}, {Indeterminate, Indeterminate}, {Indeterminate, 
  Indeterminate}, {Indeterminate, Indeterminate}, {Indeterminate, 
  Indeterminate}, {Indeterminate, Indeterminate}, {Indeterminate, 
  Indeterminate}, {Indeterminate, Indeterminate}, {Indeterminate, 
  Indeterminate}, {Indeterminate, Indeterminate}, {Indeterminate, 1}}

We see that the limit is Indeterminate inside interval (0,1). At 0 it exists only if taken limit from below and at 1 only if taken from above.

Now the same code just the expression inside limit is simplified at first:

Table[Limit[Floor[x^2 + 3 x + 1 - (x + 1)^2]/Floor[x] // FullSimplify,
     x -> p, Direction -> #] & /@ {"FromBelow", "FromAbove"}, {p, 0, 
  1, 1/10}]

---

{{1, 1}, {1, 1}, {1, 1}, {1, 1}, {1, 1}, {1, 1}, {1, 1}, {1, 1}, {1, 
  1}, {1, 1}, {1, 1}}

So Mathematica works as it should in both cases.