19

If I enter x/x, I get 1. Such behavior leads to this:

Simplify[D[Sqrt[x^2], x, x]]

0

The same would be even if I use Together instead of Simplify.

One could then think that $\sqrt{x^2}$ is doubly differentiable at least $\forall x\in\mathbb R$, but if we remove Simplify call, we would reveal that it's not:

D[Sqrt[x^2], x, x]

-(x^2/(x^2)^(3/2)) + 1/Sqrt[x^2]

Even more ridiculous is this (which I guess is because x/x is simplified before feeding to Assuming):

Assuming[x == 0, x/x]

1

Why does Mathematica assume $x\ne0$? Is there a way to make it not cancel out such terms?

Ruslan
  • 7,152
  • 1
  • 23
  • 52
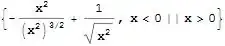
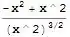
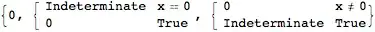
  • Well if you take a look at it, -(x^2/(x^2)^(3/2)) + 1/Sqrt[x^2] is exactly zero, except at x=0. But From a mathematical standpoint the problem is more like why does mathematicas differential operator D not exclude x=0 in this case. – Wizard Aug 16 '14 at 16:58
  • Here it's not a problem: D gives an expression, which is undefined for $x=0$. It's quite a correct result for function, which isn't differentiable at $x=0$. But then simplifying it to $0$ makes it defined at $x=0$ too, which is incorrect. – Ruslan Aug 16 '14 at 17:31
  • This is Mathematica's default behavior, so it's exactly the expected result. Any undefined symbol is assumed by Simplify to be a generic complex number. By generic, I mean not having any isolated special value, such as 0. You have to use Assumptions to change this default. – Jens Aug 16 '14 at 17:35
  • 2
    @Jens So how exactly do I use Assumptions for this? See update of the question. – Ruslan Aug 16 '14 at 17:36
  • For doing the derivative, I would perhaps approach it as shown in my answer. – Jens Aug 16 '14 at 17:42
  • By the way, the issue with Assuming in your last example is simply that $Assumptions are ignored by the expression x/x (specifically Power); only Simplify other functions that understand the option Assumptions can be affected by Assuming. This is also why the assumption of real variables in a second derivative has to be applied once in each differentiation step, which required me to split the second derivative in my answer into two first derivatives wrapped in FullSimplify. – Jens Aug 16 '14 at 21:26

3 Answers3

10

Let's define 

f[x_] := Sqrt[x^2]

FullSimplify[D[f[x],x], x ∈ Reals]

(* ==> Sign[x] *)

You can use f'[x] or D[f[x],x] interchangeably here. Then the second derivative is simply

FullSimplify[D[Sign[x], x], x ∈ Reals]

(* ==> Derivative[1][Sign][x] *)

So doing the second derivative in two steps yields a mathematically correct answer. The derivative of the Sign function is not defined, but we can define it in the sense of distributions by replacing Sign[x] with 2HeavisideTheta[x]-1. Then one would obtain this nice result for the second derivative:

FullSimplify[D[2 HeavisideTheta[x] - 1, x], 
 x ∈ Reals]

(* ==> 2 DiracDelta[x] *)

Here is my initial way to get a mathematically expected result by making the domain explicit over which the function is defined:

f[x_] := Piecewise[{{Sqrt[x^2], x > 0}, {Undefined, True}}]

Simplify[D[f[x], x, x]]

(* ==> ConditionalExpression[0, x > 0] *)

However, this is only a band-aid.

Jens
  • 97,245
  • 7
  • 213
  • 499
9
fun = Sqrt[x^2];

dd = D[fun, x, x];

With V10 we can explicitly define:

{dd, FunctionDomain[dd, x]}

enter image description here

Or

{Simplify @ dd, FunctionDomain[dd, x]}

{0, x < 0 || x > 0}

Also with V10 you might consider Inactivate:

di = D[Inactivate@Sqrt[x^2], x, x] // Together

enter image description here

which prevents Together from evaluating to 0

di // Activate

0

eldo
  • 67,911
  • 5
  • 60
  • 168
7

Here are three approaches to the function:

f1[x_] := Piecewise[{{Sqrt[x^2], x != 0}}, 0]

f2[x_] := Piecewise[{{Sqrt[x^2], x < 0}, {Sqrt[x^2], x > 0}}, 0]

f3[x_] := Piecewise[{{-x, x < 0}, {x, x > 0}}, 0]

Their second derivatives.

Simplify@D[#[x], x, x] & /@ {f1, f2, f3}

Mathematica graphics

It seems that f2 or f3 might be used, but Simplify[f2[x]] results in f1[x].

Simplify[f2[x]] // InputForm
(* Piecewise[{{Sqrt[x^2], x != 0}}, 0] *)

So if the functions are simplified, only f3 gives the correct result:

Simplify@D[Simplify@#[x], x, x] & /@ {f1, f2, f3}

Mathematica graphics

Michael E2
  • 235,386
  • 17
  • 334
  • 747
  • (+1) This is what I was aiming for (before I messed up and wrongly guessed that there was a bug in version 10)... – Jens Aug 16 '14 at 18:53