I want to make arrows with custom styles, as shown below. However, I do not know how to design these in Mathematica-12.0. I tried using Graphics, Arrow and Arrowheads, but they produce regular boring arrows.
Does anyone know how to customise these? It would be very helpful if you could at least direct me correctly.
However, as suggested by @Domen, the Custom arrow shaft question is similar to mine. However, the answer there is not complete. So, my question is justified
Clear["Global`*"];
pts = {{0,
0}, {-.5, .5}, {-.5, .25}, {-1.75, .25}, {-1.75, -.25}, {-.5, \
-.25}, {-.5, -.5}};
poly = BoundaryMeshRegion[pts,
Line@Append[#, First@#] &@Range@Length@pts];
conics =
Table[ConicHullRegion[{-1.75, h}, {{0, 0}}, {AngleVector[.02],
AngleVector[-.02]}], {h, -1, 1, .1}];
range = {{-2, 1}, {-1, 1}};
Graphics[
RegionIntersection[
BoundaryDiscretizeRegion[RegionUnion@conics, range], poly]]
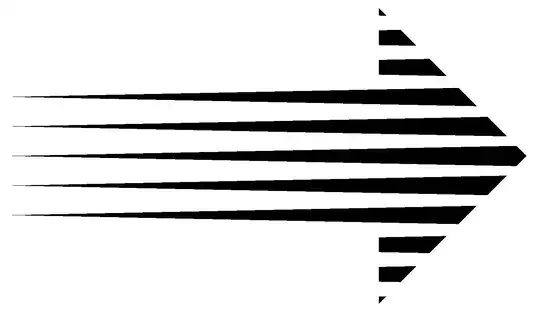
pts = {{0, 0}, {-.5, .5}, {-.5, .25}, {-1.75, .25}, {-1.5,
0}, {-1.75, -.25}, {-.5, -.25}, {-.5, -.5}};
Graphics3D[{EdgeForm[], {MaterialShading[{"Glazed", Red}], ,
RegionProduct[Polygon[pts], Point[{{0.}, {.2}}]]},
Black, {HalftoneShading[.3, Red, "Line"],
RegionProduct[RegionBoundary@Polygon[pts], Line[{{0.}, {.2}}]]}},
Lighting -> "ThreePoint", Boxed -> False]
RegionPlot3D to add shading.pts = {{0, 0}, {-.5, .5}, {-.5, .25}, {-1.75, .25}, {-1.5,
0}, {-1.75, -.25}, {-.5, -.25}, {-.5, -.5}};
side = RegionPlot3D[
RegionProduct[RegionBoundary@Polygon[pts], Line[{{0.}, {.2}}]],
MeshFunctions -> {Normalize@{1, 2, 3} . {#1, #2, #3} &},
Mesh -> 60, MeshStyle -> None, MeshShading -> {Red, Black, Red},
PlotStyle -> Red, Boxed -> False];
Graphics3D[{EdgeForm[], {MaterialShading[{"Glazed", Red}],
RegionProduct[Polygon[pts], Point[{{0.}, {.2}}]]}, First@side},
Lighting -> "ThreePoint", Boxed -> False]
Texture seems still not so perfect. ( $Version 14.0.0)Clear["Global`*"];
pts = {{0, 0}, {-.5, .5}, {-.5, .25}, {-1.75, .25}, {-1.5,
0}, {-1.75, -.25}, {-.5, -.25}, {-.5, -.5}};
side = RegionProduct[Line[Append[#, First@#] &@pts],
Line[{{0.}, {.2}}]];
pic = Graphics[{Red, HatchFilling[π/2*.88, 10, 20],
Rectangle[{0, 0}, {2, 2}]}, Background -> Black,
PlotRangePadding -> None];
Graphics3D[{EdgeForm[], {MaterialShading[{"Glazed", Red}],
RegionProduct[Polygon[pts], Point[{{0.}, {.2}}]]}, Texture[pic],
side}, Lighting -> "ThreePoint", Boxed -> False]
Clear["Global`*"];
pts = {{0, 0}, {-.5, .5}, {-.5, .25}, {-1.75, .25}, {-1.5,
0}, {-1.75, -.25}, {-.5, -.25}, {-.5, -.5}};
θ = π/3;
h = .2;
mesh[a_, b_] := Module[{e2, poly, e1, normal},
e2 = {0, 0, 1};
poly = Polygon[{a, b, b + h*e2, a + h*e2}];
e1 = Normalize[b - a];
normal =
Normalize[Cross@{Cos[θ], Sin[θ]} . {e1, e2}];
RegionPlot3D[poly, Mesh -> {Range[-10, 10, .02]},
MeshFunctions -> {normal . ({#1, #2, #3}) &},
MeshShading -> {Red, Black}, Boxed -> False]]
Graphics3D[{First /@
mesh @@@ Partition[PadRight[#, 3] & /@ pts, 2, 1, 1], Red,
PadRight[#, 3, 0] & /@ pts // Polygon,
PadRight[#, 3, h] & /@ pts // Polygon}, Boxed -> False]
Playing with ImageEffect
ImageEffect[Rasterize @
BoundaryDiscretizeGraphics[
Graphics @ Text @ Style["→", 60], _Text,
MeshCellStyle -> {2 -> Red, 1 -> None}],
{"Jitter", 10}]
Combine multiple effects ({"Jitter", 20}, {"MotionBlur", 30, Pi/6} and {"Jitter", 2}:
Fold[ImageEffect,
ImagePad[Rasterize @
BoundaryDiscretizeGraphics[
Graphics @ Text @ Style["\[RightArrow]", 72], _Text,
MeshCellStyle -> {2 -> Red, 1 -> None}],
30, White],
{{"Jitter", 20},
{"MotionBlur", 30, Pi/6},
{"Jitter", 2}}]
With pts from cvgmt's answer, an alternative way to get a 3D arrow using RegionPlot3D:
RegionPlot3D[Polygon @ Map[Append[0]] @ pts,
MaxRecursion -> 0,
"Extrusion" -> .2,
"ExtrusionStyle" -> {Red,
SurfaceAppearance["RampShading", "StepCount" -> 1,
"Tiling" -> {-20, 1}, Texture["HalftoneShadingLine"]]},
Boxed -> False,
PlotStyle -> Red,
Lighting -> "ThreePoint"]
Replace "Tiling" -> {-20, 1} with "Tiling" -> {20, 1} to get
Use "Tiling" -> {20, 0} to get
See also: RegionPlot3D KnotData
