How to make the segmentation function automatically draw the correct function image at the break point?

Question

The function is:

We know that f[x] is an even function defined on x < 0 And x > 0,

when x > 0,

0 < x <= 2, Abs[x-1],

x > 2, 1/2 f[x - 2]

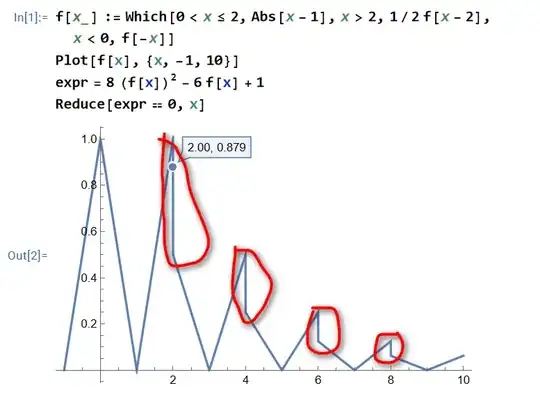
There is a problem with drawing an image of f[x] with the following code, see image drawing red circle

f[x_] := 
 Which[0 < x <= 2, Abs[x - 1], x > 2, 1/2 f[x - 2], x < 0, f[-x]]
Plot[f[x], {x, -1, 10}]

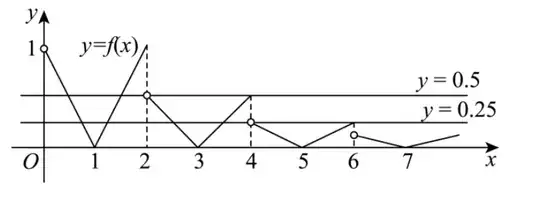
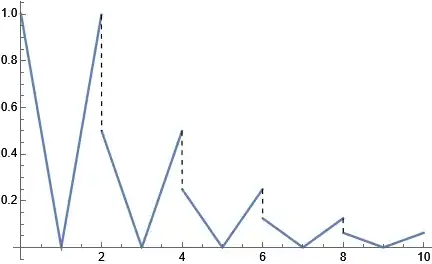
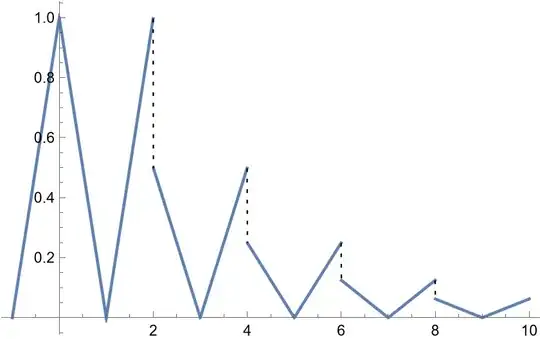
The correct image looks like this, and notice that the images at the demarcation point are not connected

How to make the segmentation function automatically draw the correct function image at the break point?

Answer 1

For now you could do this workaround but this can be automated if needed. Left as an exercise.

f[x_] := Which[0 < x < 2, Abs[x - 1], x > 2, 1/2  f[x - 2],x < 0, f[-x]]
Plot[f[x], {x, 0, 10}, Exclusions -> Range[2, 10, 2]]

You can add

Plot[f[x], {x, 0, 10}, Exclusions -> Range[2, 10, 2], 
 ExclusionsStyle -> Dashed]

Answer 2

If you define your function such that it contains the discontinuities then Mma will automatically exclude them.

The function is piecewise right continuous with modulo 2 step size and vertical shrinking factor of $\frac{1}{2}^n$ where $n$ is the number of steps.

First define the base function with the left side discontinuity.

f1[x_] :=
 Piecewise[{
   {Abs[x - 1], 0 < x <= 2}
   , {Indeterminate, True}
   }]

Next apply the modulo 2 step size and the step dependent shrinking factor.

f2[x_] := f1[Mod[Abs[x], 2]]/(2^Floor[Abs[x]/2])

Mathematica will automatically exclude the discontinuities. You only need provide an exclusion style if you want to show them.

Plot[f2[x], {x, -1, 10}, ExclusionsStyle -> {Dashing[Small], None}]

Hope this helps.