Why can't I use logic operator Or to specify multiple events with WhenEvent?

Question

I want to use logic operator Or to specify multiple events.

After reading these very helpful posts here and here, it seems to be better to use a function to inlude multiple events.

But my code still fails to detect the event.

Although a list of event can be used equivalently in my problem, but I still want the logic operator version.

Thanks!

event[x_] := x == 1/2 || x == -(1/4)
sol = NDSolve[
   {x'[t] == -3 x[t], y[t] + x[t] == 1, x[0] == 1, y[0] == 0
    , WhenEvent[event[x[t]], x'[t] -> y'[t]](*fails*)
    (*,WhenEvent[{x[t]\[Equal]1/2,x[t]\[Equal]-1/4},x'[t]\[Rule]y'[
    t]]*)(*works*)
    }, {x[t], y[t]}, {t, 0, 1}, 
   Method -> {"EquationSimplification" -> "Residual"}];
Plot[{x[t], y[t]} /. sol // Evaluate, {t, 0, 1}, PlotRange -> All, 
 PlotLegends -> {"x", "y"}, PlotStyle -> {Blue, {Red, Dashed}}]

Answer 1

After reading these very helpful posts here and here, it seems to be better to use a function to inlude multiple events.

This conclusion is definitely wrong. Please notice the posts you've found are about using And (&&) to construct event, which has its particularity. (If you're interested in this topic, I'd suggest reading this post together with the comments therein also. )

As to your problem, it's just because the general condition in your code is too hard to satisfy. When a ODE/DAE system is solved by NDSolve, function values are only obtained at discretized grid points, so the x == 1/2 || x == -(1/4) will almost never be True. And defining the condition as a general condition involving || will stop NDSolve from analyzing the condition. Please read Details and Options section of document of WhenEvent carefully for more info… OK, let me add an example:

func[x_] := x == 1/2
event1 = WhenEvent[func@x[t], "StopIntegration"]
(* WhenEvent[func[x[t]], "StopIntegration"] *)
event2 = WhenEvent[func@x[t] // Evaluate, "StopIntegration"]
(* WhenEvent[x[t] == 1/2, "StopIntegration"] *)
lst = 
  NDSolveValue[{x'[t] == 1, x[0] == 0, #}, x, {t, 0, 1}] & /@ {event1, event2};
ListPlot[#, PlotRange -> {{0, 1}, {0, 1}}] & /@ lst

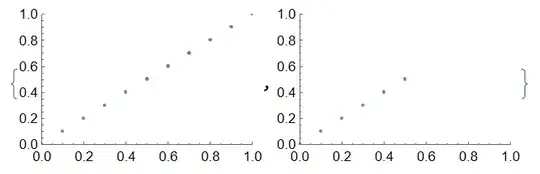
As we can see, event1 and event2 seem to be the same, but only event2 manages to stop the calculation when x[t] == 1/2. This is because in event1, the condition x[t] == 1/2 is hidden in func[x[t]], so NDSolve cannot see it. NDSolve will then try to handle it in a general manner i.e. checking for the point where the func[x[t]] becomes True: this almost never happen! But event2 is different, in this case NDSolve can see the condition is an equation, so it can use root searching technique to find the t that satisfies the equation.

"OK, so you mean an Evaluate will fix the code?" Sadly it won't help in your case, because currently only conditions in the first table in Details and Options section of document of WhenEvent i.e. f == 0, f > 0, f < 0, Mod[…] == 0 and And are analyzed in special manner by NDSolve AFAIK, so your event involving Or (||) won't be cleverly analyzed even if we add Evaluate.

In my opinion, using a list of event is the way to go here. Why do you want to avoid this? Anyway, if you insist, one work-around is to, as shown in the posts you've found, use inequality to construct a general condition that's easier to satisfy:

event[x_] := 0 <= x <= 1/2 || 0 >= x >= -(1/4)
sol = NDSolve[{x'[t] == -3  x[t], y[t] + x[t] == 1, x[0] == 1, y[0] == 0, 
    WhenEvent[event[x[t]], x'[t] -> y'[t]]
    }, {x[t], y[t]}, {t, 0, 1}, Method -> {"EquationSimplification" -> "Residual"}];
Plot[{x[t], y[t]} /. sol // Evaluate, {t, 0, 1}, PlotRange -> All, 
 PlotLegends -> {"x", "y"}, PlotStyle -> {Blue, {Red, Dashed}}]