How to evaluate conditional roots in ContourPlot3D?

Question

I have the following Mathematica code:

$Assumptions = {r ∈ Reals, r >= 0, rh ∈ Reals, 
   rh > 0, Q ∈ Reals, 
   Q >= 0, α ∈ Reals, α > 0, 
   P ∈ Reals, P >= 0, L ∈ Reals, L > 0};
M[rh_, Q_, 
   P_] = (3 \[Pi] rh^2)/
    8 (1 + (2 α)/rh^2 + (4 \[Pi] P rh^2)/3) + (\[Pi] Q^2)/(
   8 rh^2);
f[r_] = 1 + 
   r^2/(4 α) (1 - 
      Sqrt[1 + (64 α M[rh, Q, P])/(3 Pi r^4) - (
        8 α Q^2)/(3 r^6) - (32 Pi α P)/3]);
T[rh_, Q_, P_] = -((Q^2 - 3 rh^4 - 8 P \[Pi] rh^6)/(
   6 \[Pi] rh^5 + 24 \[Pi] rh^3 α));
rhmin = SolveValues[T[rh, Q, P] == 0, rh, Reals][[1]];
Veff[r_] = f[r] (L^2/r^2 - ϵ) // FullSimplify;
L = 20; P = 1/10; α = 1/100; Q = 1/5; ϵ = -1;
sol = SolveValues[Veff'[r] == 0, r, Reals][[3 ;; 5]];
Plot[sol, {rh, rhmin, sol[[2, 2, 2, 5]]}]

which gives me the following output:

If I try to use the same logic to create a ContourPlot3D,

ContourPlot3D[
 Evaluate@{r == sol[[1, 1]], r == sol[[2, 1]], r == sol[[3, 1]]}, {rh,
   rhmin, sol[[2, 2, 2, 5]]}, {r, rh, 5}, {z, 0, 1}]

I get inaccurate results, primarily because of the conditions attached to the roots, as shown below:

Is there a way I can incorporate the conditions along with the roots in the ContourPlot3D to get a result like the one shown below? This question is also a continuation of the one asked here.

Ulrich Neumann · Answer 1 · 2024-02-22T14:09:52.327

1

Try

fun = Function[{r, rh}, Evaluate[Simplify[Veff'[r ]]]]
ContourPlot[fun[r, rh] == 0, {r, 0.5, 2}, {rh, 0, 1.2}, FrameLabel -> {r, rh}]

ContourPlot3D[fun[r, rh] == 0, {r, 0.5, 2}, {rh, 0, 1.2}, {z, 0, 1},AxesLabel -> {r, rh, z}]

addendum

Plot3D[f[r] (L^2/r^2 - \[Epsilon]), {r, rhmin, 2}, {rh, 0.01,1.63592}, 
MeshFunctions -> Function[{r, rh}, fun[r, rh]],Mesh -> {{0}},MeshStyle -> Red, PlotRange -> Automatic,AxesLabel -> {r, rh, "f[r] (L^2/r^2 - \[Epsilon])"}]

edited Feb 22 '24 at 14:09

answered Feb 22 '24 at 09:32

Ulrich Neumann

53,729
2
23
55

Oh basically switching the position of r and rh. Though it works, aren't both results different? Since in the first r depends on the rh initials and in the second there is no such dependence. – codebpr Feb 22 '24 at 12:49
I think both results aren't different. Look at the 3D-plot in z-direction. – Ulrich Neumann Feb 22 '24 at 13:45
But if I tweak your code to change the range to say, {r, rhmin, 5}, {rh, rhmin, 1.63592}, {z, 0, 1}, I get a different result even when the range is the same. My ultimate aim is to project the extrema of the Veff[r] below it's 3D plot for different Black Holes as originally asked here. – codebpr Feb 22 '24 at 13:58
@codebpr See my addendum which shows the surface f[r] (L^2/r^2 - \[Epsilon]) and the extrema. – Ulrich Neumann Feb 22 '24 at 14:11
Your addendum gives a very different 3d plot than mine. If I use your code with mesh functions and tweak it a bit like this: Plot3D[f[r] (L^2/r^2 - \[Epsilon]), {rh, rhmin, 1.63592}, {r, rh, 6}, MeshFunctions -> Function[{r, rh}, fun[r, rh]], Mesh -> {{0}}, MeshStyle -> Red, PlotRange -> {0, 700}, AxesLabel -> {r, rh, "f[r] (L^2/r^2 - \[Epsilon])"}] I get the correct 3D plot but here the Mesh function which marks the extrema doesn't seem to work. – codebpr Feb 22 '24 at 14:21
Can you reproduce Plot3D... in my answer (rhmin==0.332372)? – Ulrich Neumann Feb 22 '24 at 15:13
Sure, If I use your original answer, and use this: `p = Plot3D[Veff[r], {rh, rhmin, 2}, {r, rh, 6}, PlotRange -> {-300, 700}, AxesLabel -> {rh, r, "Veff(r)"}];
belt = ContourPlot3D[ fun[r, rh] == 0, {r, 0.5, 2}, {rh, 0, 1.2}, {z, -250, -300}]; Show[p, belt]`, I get this
– codebpr Feb 22 '24 at 15:43
My question was: Can you reproduce the Plot3D in my answer! – Ulrich Neumann Feb 22 '24 at 16:26
I think that's the main issue. You take r before rh, while I use rh first and then r ranges from {r, rh, 6} so they are both different data which can also be seen from the Table itself. – codebpr Feb 22 '24 at 16:36
1

In this case you have to change MeshFunctions -> Function[{rh, r}, fun[r, rh]] – Ulrich Neumann Feb 22 '24 at 17:21
Yes now it works! Thanks! – codebpr Feb 23 '24 at 04:49

score 1 · Accepted Answer · answered Feb 22 '24 at 18:50

OP's original code:

$Assumptions = {r \[Element] Reals, r >= 0, rh \[Element] Reals, 
   rh > 0, Q \[Element] Reals, 
   Q >= 0, \[Alpha] \[Element] Reals, \[Alpha] > 0, 
   P \[Element] Reals, P >= 0, L \[Element] Reals, L > 0};
M[rh_, Q_, 
   P_] = (3 \[Pi] rh^2)/
     8 (1 + (2 \[Alpha])/rh^2 + (4 \[Pi] P rh^2)/
       3) + (\[Pi] Q^2)/(8 rh^2);
f[r_] = 1 + 
   r^2/(4 \[Alpha]) (1 - 
      Sqrt[1 + (64 \[Alpha] M[rh, Q, 
            P])/(3 Pi r^4) - (8 \[Alpha] Q^2)/(3 r^6) - (32 Pi \
\[Alpha] P)/3]);
T[rh_, Q_, 
   P_] = -((Q^2 - 3 rh^4 - 8 P \[Pi] rh^6)/(6 \[Pi] rh^5 + 
       24 \[Pi] rh^3 \[Alpha]));
rhmin = SolveValues[T[rh, Q, P] == 0, rh, Reals][[1]];
Veff[r_] = f[r] (L^2/r^2 - [Epsilon]) // FullSimplify;
L = 20; P = 1/10; [Alpha] = 1/100; Q = 1/5; [Epsilon] = -1;
sol = SolveValues[Veff'[r] == 0, r, Reals][[3 ;; 5]];

Plot:

Plot[sol, {rh, 0, 1.6359193838319277`}]

ContourPlot:

  style1 = Directive[Specularity[GrayLevel[1], 3], RGBColor[
   0.368417, 0.506779, 0.709798], 
   Lighting -> {{"Ambient", RGBColor[
      0.19699838300000003`, 0.252204821, 
       0.33320940200000004`]}, {"Directional", RGBColor[
      0.15473514000000002`, 0.21284718000000002`, 
       0.29811516000000005`], ImageScaled[{0, 2, 2}]}, {"Directional",
       RGBColor[
      0.15473514000000002`, 0.21284718000000002`, 
       0.29811516000000005`], ImageScaled[{2, 2, 2}]}, {"Directional",
       RGBColor[
      0.15473514000000002`, 0.21284718000000002`, 
       0.29811516000000005`], ImageScaled[{2, 0, 2}]}}];
style2 = Directive[Specularity[GrayLevel[1], 3], RGBColor[
   0.880722, 0.611041, 0.142051], 
   Lighting -> {{"Ambient", RGBColor[
      0.30100577, 0.22414668499999998`, 0.090484535]}, {"Directional",
       RGBColor[0.2642166, 0.18331229999999998`, 0.04261530000000001],
       ImageScaled[{0, 2, 2}]}, {"Directional", RGBColor[
      0.2642166, 0.18331229999999998`, 0.04261530000000001], 
      ImageScaled[{2, 2, 2}]}, {"Directional", RGBColor[
      0.2642166, 0.18331229999999998`, 0.04261530000000001], 
      ImageScaled[{2, 0, 2}]}}];
style3 = Directive[Specularity[GrayLevel[1], 3], RGBColor[
   0.560181, 0.691569, 0.194885], 
   Lighting -> {{"Ambient", RGBColor[
      0.1830429875, 0.21424763749999998`, 
       0.0962851875]}, {"Directional", RGBColor[
      0.14004525, 0.17289224999999997`, 0.048721249999999994`], 
      ImageScaled[{0, 2, 2}]}, {"Directional", RGBColor[
      0.14004525, 0.17289224999999997`, 0.048721249999999994`], 
      ImageScaled[{2, 2, 2}]}, {"Directional", RGBColor[
      0.14004525, 0.17289224999999997`, 0.048721249999999994`], 
      ImageScaled[{2, 0, 2}]}}];
pl1 = sol[[1, 1]];
pl2 = sol[[2, 1]];
pl3 = sol[[3, 1]];
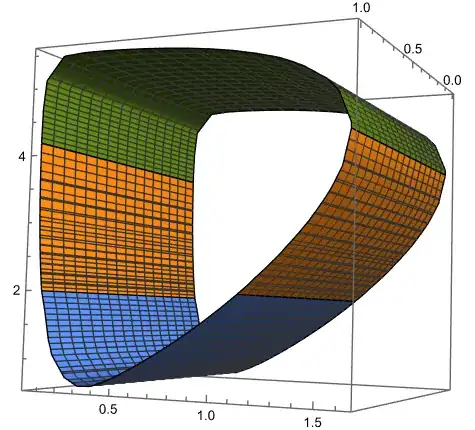
Show[ContourPlot3D[
  r == pl1, {rh, 0.08352936846427979, 1.1186546369028976}, {r, rh, 
   6}, {z, 0, 1}, ContourStyle -> style1], 
 ContourPlot3D[
  r == pl2, {rh, 1.1186546369028976, 1.6359193838319277}, {r, rh, 
   6}, {z, 0, 1}, ContourStyle -> style2], 
 ContourPlot3D[
  r == pl2, {rh, 0.048454562655432167, 0.08352936846427979}, {r, rh,
    6}, {z, 0, 1}, ContourStyle -> style2], 
 ContourPlot3D[
  r == pl3, {rh, 0.048454562655432167, 1.6359193838319277}, {r, rh, 
   6}, {z, 0, 1}, ContourStyle -> style3], PlotRange -> All]
ContourPlot3D[
 Veff'[r] == 0, {rh, 0.048454562655432167, 1.6359193838319277}, {r, 
  rh, 6}, {z, 0, 1}]

Thank you for the answer! It works, actually the minimum value of rh is not 0 in my plot but rhmin maybe that's why a different result. Changing that gives me the desired plot. Just one query, in your last code if I increase the PlotPoints to say 30, I get some undesired branches, how to get rid of them: ContourPlot3D[ Veff'[r] == 0, {rh, rhmin, 1.6359193838319277}, {r, rh, 6}, {z, 0, 1}, PlotPoints -> 30] giving this. — codebpr, Feb 23 '24 at 05:07
@codebpr: ContourPlot plots all solutions. The branches are solution to your equation too. — azerbajdzan, Feb 23 '24 at 10:46

How to evaluate conditional roots in ContourPlot3D?

2 Answers2