I've checked all of those; I am not quite sure if any of them have the
time as the x-axis
The syntax to generate phase plot for first order ode of form
$$
y'(x) = \frac{A(x,y)}{B(x,y)}
$$
is
StreamPlot[{B,A},{x,from,to},{y,from,to}]
So using the above on your ode, where now y is your v and x is your t gives
\begin{align*}
\frac{dv}{dt} &= g - \frac{k}{m}v^2\\
&= \frac{g - \frac{k}{m}v^2}{1}
\end{align*}
Hence setting some values for g and m and k gives
g = 9.81; m = 10; k = 0.1;
StreamPlot[{1, g - k/m*v^2}, {t, 0, 10}, {v, -10, 10},
FrameLabel -> {"t", "v(t)"}, BaseStyle -> 20]
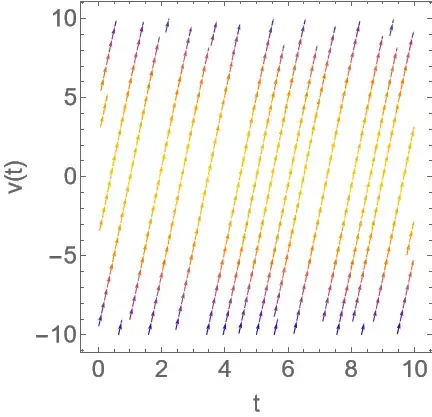
The above shows solutions curves. If you have a specific IC, then one of these curves will be the solution.
Here is a Manipulate to make it easier to analyze the system
Manipulate[
Module[{g = 9.81},
StreamPlot[{1, g - k/m*v^2}, {t, 0, maxtime}, {v, -maxV, maxV},
FrameLabel -> {"t", "v(t)"}, BaseStyle -> 20]
]
,
{{m, 10, "mass"}, 0.1, 100, .1, Appearance -> "Labeled"},
{{k, 1, "stiffness k"}, 0.1, 10, .1, Appearance -> "Labeled"},
{{maxtime, 1, "time range"}, 0.01, 10, .01,
Appearance -> "Labeled"},
{{maxV, 1, "velocity range"}, 0.01, 30, .01, Appearance -> "Labeled"},
TrackedSymbols :> {m, k, maxtime, maxV}
]
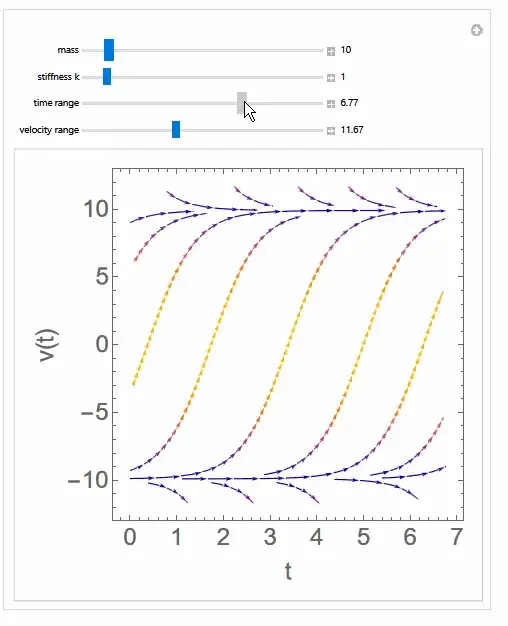


Also check this.
– codebpr Mar 04 '24 at 05:49