46

I'm trying to plot a phase portrait for the differential equation $$x'' - (1 - x^2) x' + x = 0.5 \cos(1.1 t)\,.$$ The primes are derivatives with respect to $t$. I've reduced this second order ODE to two first order ODEs of the form $ x_1' = x_2$ and $x_2' - (1 - x_1^2) x_2 + x_1 = 0.5 \cos(1.1 t)$. Now I wish to use mathematica to plot a phase portrait. Unfortunately, I'm unsure of how to do this because of the dependence of the second equation on an explicit $t$.

LCarvalho
  • 9,233
  • 4
  • 40
  • 96
covertbob
  • 617
  • 1
  • 7
  • 6
  • 1
    Have a look at ParametricPlot. – b.gates.you.know.what Nov 05 '12 at 18:42
  • 1
    you could look at this as well? http://mathematica.stackexchange.com/questions/14027/how-do-i-plot-xt-vs-xt-where-xt-and-xt-are-solutions-to-ndsolve/14029#14029 – chris Nov 05 '12 at 18:43
  • Chris, this is much to complicated for me. I'm a huge mathematica newb. Could you explain more precisely? – covertbob Nov 05 '12 at 18:46
  • 5
    @covertbob If you're that new to Mathematica, then I suggest going through some tutorials and using the virtual book. Also see this answer for some introductory materials. Unfortunately, this site is not the place to learn Mathematica step-by-step from scratch. For starters, you can look at the code in the answer Chris linked to, and use the documentation center to read up on the functions used (e.g., NDSolve, ParametricPlot, StreamPlot, etc.) Just the first two should be sufficient for you to make headway on your problem. – rm -rf Nov 05 '12 at 18:55
  • Not an answer to your question - just a bunch of pretty phase portrait pictures - see http://drorbn.net/AcademicPensieve/Classes/12-267/QuadraticPortraits.html. The Mathematica notebook that produced the picture is linked at the bottom of that URL. – Dror Bar-Natan Nov 08 '12 at 22:07

3 Answers3

47

again just a slight modification from the documentation 

splot = StreamPlot[{y, (1 - x^2) y - x}, {x, -4, 4}, {y, -3, 3}, 
   StreamColorFunction -> "Rainbow"];
Manipulate[
 Show[splot, 
  ParametricPlot[
   Evaluate[
    First[{x[t], y[t]} /. 
      NDSolve[{x'[t] == y[t], 
        y'[t] == y[t] (1 - x[t]^2) - x[t] + 0.5 Cos[1.1 t], 
        Thread[{x[0], y[0]} == point]}, {x, y}, {t, 0, T}]]], {t, 0, 
    T}, PlotStyle -> Red]], {{T, 20}, 1, 100}, {{point, {3, 0}}, 
  Locator}, SaveDefinitions -> True]

Mathematica graphics

Or just to show off (again a rip off from the documentation)

splot = LineIntegralConvolutionPlot[{{y, (1 - x^2) y - x}, {"noise", 
     1000, 1000}}, {x, -4, 4}, {y, -3, 3}, 
   ColorFunction -> "BeachColors", LightingAngle -> 0, 
   LineIntegralConvolutionScale -> 3, Frame -> False];
Manipulate[
 Show[splot, 
  ParametricPlot[
   Evaluate[
    First[{x[t], y[t]} /. 
      NDSolve[{x'[t] == y[t], y'[t] == y[t] (1 - x[t]^2) - x[t]+0.5 Cos[1.1 t], 
        Thread[{x[0], y[0]} == point]}, {x, y}, {t, 0, T}]]], {t, 0, 
    T}, PlotStyle -> White]], {{T, 20}, 1, 100}, {{point, {3, 0}}, 
  Locator}, SaveDefinitions -> True]

Mathematica graphics

chris
  • 22,860
  • 5
  • 60
  • 149
  • Just a question. Is it right, that StreamPlot[{v1[x,y],v2[x,y]}] returns a set of solutions of the differential equations x'=v1; y'=v2? It looks like an elementary information that everybody knows. But it happened that I do not know, and there is no explicit discussion of this point in the Help/StreamPlot. Please let me know. Where could I have a look at the proof, or at least, an explanation? If I understand right, the StreamPlot simply yields the phase portrait, does it? – Alexei Boulbitch Nov 06 '12 at 10:51
  • @AlexeiBoulbitch yes it yields a set of solutions for the homogenous set of equations. But it does not attempt to be continuous. In the previous example if you remove + 0.5 Cos[1.1 t] you will see that the red curve and the underlying flow become identical. – chris Nov 07 '12 at 17:48
42

The EquationTrekker package is a great package for plotting and exploring phase space

<< EquationTrekker`
EquationTrekker[x''[t] - (1 - x[t]^2) x'[t] + x[t] == 0.5 Cos[1.1 t], x[t], {t, 0, 10}]

This brings up a window where you can right click on any point and it plots the trajectory starting with that initial condition:

enter image description here

You can do more as well, such as add parameters to your equations and see what happens to the trajectories as you vary them:

 EquationTrekker[x''[t] - (1 - x[t]^2) x'[t] + x[t] == a Cos[\[Omega] t],
                 x[t], {t, 0, 10}, TrekParameters -> {a -> 0.5, \[Omega] -> 1.1}
                ]

enter image description here

David Slater
  • 1,525
  • 10
  • 13
  • 3
    This no longer works in the version I have, 11.0.0.0. It produces error messages and no output. This is what has happened every time I've tried a Mathematica package. They always seem to fail in the version I am using. Sometimes I can fix the resulting errors, but usually not. In the end I always have to go back to built-in functionality, which seldom fails in my experience. – Ralph Dratman Apr 04 '17 at 23:36
  • Hi, this package has a large number of errors in version 12.1 and cannot be used. – A little mouse on the pampas Jul 24 '20 at 01:01
  • 1
    See https://mathematica.stackexchange.com/questions/92810/equationtrekker-using-mathematica-10-2 for more about how to use EquationTrekker in versions since V10.2 – Michael E2 Nov 01 '20 at 00:40
26

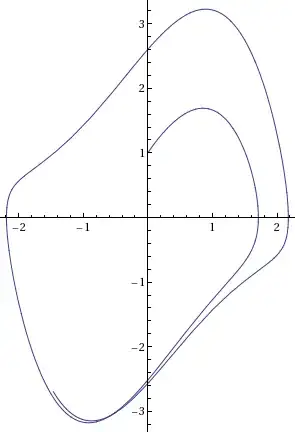
You can solve the equation with (you might want to change the initial conditions) :

sol[t_] =  NDSolve[{x''[t] - (1 - x[t]^2) x'[t] + x[t] == 0.5 Cos[1.1 t], 
   x[0] == 0, x'[0] == 1}, x[t], {t, 0, 10}][[1, 1, 2]]

Now you can use the solution as any other function; in particular, you can plot it versus its derivative :

ParametricPlot[{sol[t], sol'[t]}, {t, 0, 10}]

enter image description here

b.gates.you.know.what
  • 20,103
  • 2
  • 43
  • 84